题目内容
10．已知函数y=$\left\{\begin{array}{l}{2x+1（x≥0）}\\{4x（x＜0）}\end{array}\right.$，当x=2时，函数值y为（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
分析 利用已知函数关系式结合x的取值范围，进而将x=2代入求出即可．
解答 解：∵x≥0时，y=2x+1，
∴当x=2时，y=2×2+1=5．
故选：A．
点评 此题主要考查了函数值，注意x的取值不同对应函数解析式不同，进而得出是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
18．式子2$\sqrt{3}$+$\sqrt{2}$的结果精确到0.01为（可用计算器计算或笔算）（ ）
| A． | 4.9 | B． | 4.87 | C． | 4.88 | D． | 4.89 |
15．化简$\frac{2x}{{x}^{2}+2x}$-$\frac{x-6}{{x}^{2}-4}$的结果为（ ）
| A． | $\frac{1}{{x}^{2}-4}$ | B． | $\frac{1}{{x}^{2}+2x}$ | C． | $\frac{1}{x-2}$ | D． | $\frac{x-6}{x-2}$ |
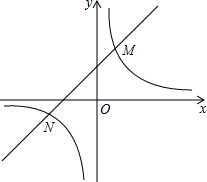如图，反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于M（1，3），N两点，点N的横坐标为-3．