题目内容
14.用适当的方法解下列方程(1)x2-14x=8
(2)2x2-9x+8=0
(3)4x(2x+1)=3(2x+1)
(4)(x+1)2-3(x+1)+2=0.
分析 (1)把方程左边加上一次项系数一半的平方,利用配方法解方程即可;
(2)首先找出a=2,b=-9,c=8,利用公式法解方程即可;
(3)提取公因式(2x+1),即可得到(2x+1)(4x-3)=0,再解两个一元一次方程即可;
(4)把(x+1)看一个整体,利用分解因式法解一元二次方程即可.
解答 解:(1)∵x2-14x=8,
∴x2-14x+72=8+72,
∴(x-7)2=57,
∴x1=7+$\sqrt{57}$,x2=7-$\sqrt{57}$;
(2)∵2x2-9x+8=0,a=2,b=-9,c=8,
∴b2-4ac=81-4•2•8=17,
∴x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{-(-9)±\sqrt{17}}{2•2}$=$\frac{9±\sqrt{17}}{4}$,
∴x1=$\frac{9+\sqrt{17}}{4}$,x2=$\frac{9-\sqrt{17}}{4}$;
(3)∵4x(2x+1)=3(2x+1)
∴(2x+1)(4x-3)=0,
∴2x+1=0 或4x-3=0,
∴x1=-$\frac{1}{2}$,x2=$\frac{3}{4}$;
(4)∵(x+1)2-3(x+1)+2=0,
∴(x+1-1)(x+1-2)=0,
∴x(x-1)=0,
∴x1=0,x2=1.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
2.下列各式中书写正确的是( )
| A. | xy2 | B. | $1\frac{1}{2}$ab | C. | $\frac{mn}{4}$ | D. | 5÷a |
19. 数a,b在数轴上的位置如图所示,则-a-b是( )
数a,b在数轴上的位置如图所示,则-a-b是( )
 数a,b在数轴上的位置如图所示,则-a-b是( )
数a,b在数轴上的位置如图所示,则-a-b是( )| A. | 正数 | B. | 零 | C. | 负数 | D. | 都有可能 |
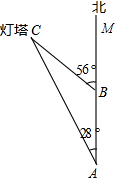 如图,14:00时,一条船从A处出发,以18海里/小时的速度,向正北航行,16:00时,船到达B处,从A处测得灯塔C在北偏西28°,从B处测得灯塔C在北偏西56°,求B处到灯塔C的距离.
如图,14:00时,一条船从A处出发,以18海里/小时的速度,向正北航行,16:00时,船到达B处,从A处测得灯塔C在北偏西28°,从B处测得灯塔C在北偏西56°,求B处到灯塔C的距离.