题目内容
12.因式分解(1)m2-n2+2m-2n
(2)x2(y2-1)+2x(y2-1)+(y2-1)
分析 (1)当被分解的式子是四项时,应考虑运用分组分解法进行分解.本题中m2-n2符合平方差公式,2m-2n提公因式后作为一项可进行下一步分解;
(2)利用提取公因式法进行因式分解;然后利用平方差公式和完全平方公式继续进行分解.
解答 解:(1)m2-n2+2m-2n,
=(m-n)(m+n)+2(m-n),
=(m-n)(m+n+2).
(2)x2(y2-1)+2x(y2-1)+(y2-1)
=(y2-1)(x2+2x+1),
=(y+1)(y-1)(x+1)2.
点评 本题考查了分组分解法分解因式,难点是采用两两分组还是三一分组.比如本题有a的二次项,a的一次项,有常数项,所以首要考虑的就是三一分组.

练习册系列答案
相关题目
2.下列各式中书写正确的是( )
| A. | xy2 | B. | $1\frac{1}{2}$ab | C. | $\frac{mn}{4}$ | D. | 5÷a |
20.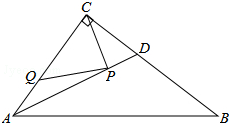 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是△ABC的角平分线,若P,Q分别是AD和AC边上的动点,则PC+PQ的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是△ABC的角平分线,若P,Q分别是AD和AC边上的动点,则PC+PQ的最小值是( )
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是△ABC的角平分线,若P,Q分别是AD和AC边上的动点,则PC+PQ的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是△ABC的角平分线,若P,Q分别是AD和AC边上的动点,则PC+PQ的最小值是( )| A. | $\frac{6}{5}$ | B. | 2 | C. | $\frac{12}{5}$ | D. | $\frac{5}{2}$ |
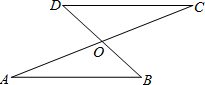 已知,如图,AC和BD相交于点O,OA=OC,OB=OD,求证:AB∥CD.
已知,如图,AC和BD相交于点O,OA=OC,OB=OD,求证:AB∥CD.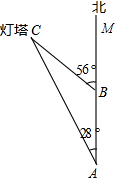 如图,14:00时,一条船从A处出发,以18海里/小时的速度,向正北航行,16:00时,船到达B处,从A处测得灯塔C在北偏西28°,从B处测得灯塔C在北偏西56°,求B处到灯塔C的距离.
如图,14:00时,一条船从A处出发,以18海里/小时的速度,向正北航行,16:00时,船到达B处,从A处测得灯塔C在北偏西28°,从B处测得灯塔C在北偏西56°,求B处到灯塔C的距离.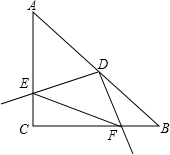 如图所示,在Rt△ABC中,AC=BC=4,∠C=90°,D为AB中点,以点D为顶点的动角∠EDF绕D点旋转,与边AC交于点E,与边BC交于点F.求证:
如图所示,在Rt△ABC中,AC=BC=4,∠C=90°,D为AB中点,以点D为顶点的动角∠EDF绕D点旋转,与边AC交于点E,与边BC交于点F.求证: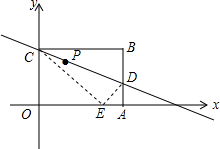 如图,在平面直角坐标系中,矩形OABC的顶点A(10,0),C(0,8),现将矩形OABC沿直线CD折叠,使点B落在x轴上的E处.
如图,在平面直角坐标系中,矩形OABC的顶点A(10,0),C(0,8),现将矩形OABC沿直线CD折叠,使点B落在x轴上的E处.