题目内容
16.有一个二次函数y=a(x-k)2的图象,三位同学分别说出了它的一些特点:甲:开口向上;
乙:对称轴是x=2;
丙:与y轴的交点到原点的距离为2.
请你写出满足上述全部特点的二次函数的解析式.
分析 由开口向上,可知a>0,对称轴是直线x=2,可得k=2,与y轴的交点到原点的距离为2,可得与y轴的交点的坐标为(0,±2),利用待定系数法求出解析式.
解答 解:∵二次函数y=a(x-k)2的图象开口向上,
∴a>0,
∵对称轴为直线x=2,
∴k=2,
∴二次函数y=a(x-k)2的解析式为y=a(x-2)2,
∵与y轴的交点到原点的距离为2,
∴与y轴交于点(0,2)或(0,-2),
把(0,2)代入得,2=4a,
∴a=$\frac{1}{2}$,
把(0,-2)代入得,-2=4a,
∴a=-$\frac{1}{2}$(舍去)
∴解析式为:y=$\frac{1}{2}$(x-2)2.
点评 本题主要考查用待定系数法求二次函数的解析式,此题是开放题,解题的关键理解题意.还要注意利用待定系数法求函数解析式,当题目中出现二次函数与x轴的交点坐标时,采用交点式比较简单.

练习册系列答案
相关题目
13.下列语句正确的是( )
| A. | $\frac{125}{216}$的立方根是±$\frac{5}{6}$ | B. | -3是27的负的立方根 | ||
| C. | $\sqrt{64}$的立方根是2 | D. | (-1)2的立方根是-1 |
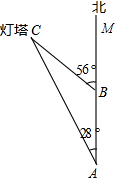 如图,14:00时,一条船从A处出发,以18海里/小时的速度,向正北航行,16:00时,船到达B处,从A处测得灯塔C在北偏西28°,从B处测得灯塔C在北偏西56°,求B处到灯塔C的距离.
如图,14:00时,一条船从A处出发,以18海里/小时的速度,向正北航行,16:00时,船到达B处,从A处测得灯塔C在北偏西28°,从B处测得灯塔C在北偏西56°,求B处到灯塔C的距离. 如图,AB是⊙O的直径,C是⊙O上的一点,AD垂直于过点C的切线,垂足为D,∠BAD=70°,则∠DAC=35°.
如图,AB是⊙O的直径,C是⊙O上的一点,AD垂直于过点C的切线,垂足为D,∠BAD=70°,则∠DAC=35°.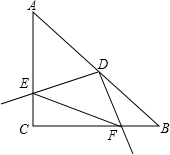 如图所示,在Rt△ABC中,AC=BC=4,∠C=90°,D为AB中点,以点D为顶点的动角∠EDF绕D点旋转,与边AC交于点E,与边BC交于点F.求证:
如图所示,在Rt△ABC中,AC=BC=4,∠C=90°,D为AB中点,以点D为顶点的动角∠EDF绕D点旋转,与边AC交于点E,与边BC交于点F.求证: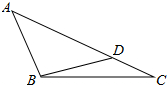 已知:如图,在△ABC中,AC=9,BC=6,请问,在边AC上是否存在一点D,使△ABC∽△BDC?若存在请求出CD的长,若不存在,请说明理由.
已知:如图,在△ABC中,AC=9,BC=6,请问,在边AC上是否存在一点D,使△ABC∽△BDC?若存在请求出CD的长,若不存在,请说明理由.