题目内容
2.用图象法解下列二元一次方程组:(1)$\left\{\begin{array}{l}{x-y=5}\\{y=3-x}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+3y=5}\\{3x-y=2}\end{array}\right.$.
分析 (1)先利用描点法画出函数x-y=5和函数y=3-x的图象,然后确定它们的交点坐标,再利用函数图象交点坐标为两函数解析式组成的方程组的解即可得到答案;
(2)先利用描点法画出函数2x+3y=5和函数3x-y=2的图象,然后确定它们的交点坐标,再利用函数图象交点坐标为两函数解析式组成的方程组的解即可得到答案.
解答 解:(1)如图,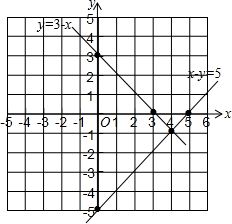
直线x-y=5和直线y=3-x的交点坐标为(4,-1),
所以方程组$\left\{\begin{array}{l}{x-y=5}\\{y=3-x}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$;
(2)如图,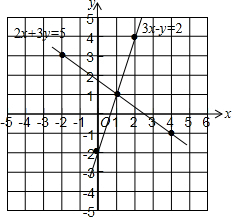
直线2x+3y=5和直线3x-y=2的交点坐标为(1,1),
所以方程组$\left\{\begin{array}{l}{2x+3y=5}\\{3x-y=2}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$..
点评 本题主要考查了一次函数与二元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
11.计算1-a-a(1-a)-a(1-a)2-a(1-a)3-…-a(1-a)2013-[(1-a)2014-3]的结果为( )
| A. | 3 | B. | 1 | C. | (1-a)2015 | D. | (1-a)2015+3 |
 如图,若将抛物线y=(x+1)2-7沿x轴平移经过点P(-2,2),求平移后抛物线的解析式.
如图,若将抛物线y=(x+1)2-7沿x轴平移经过点P(-2,2),求平移后抛物线的解析式.