题目内容
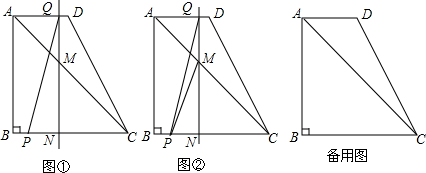
13. 已知:如图,AB=CD,AB∥CD,DE⊥AC,BF⊥AC,E、F是垂足,AF=5,求CE的长.
已知:如图,AB=CD,AB∥CD,DE⊥AC,BF⊥AC,E、F是垂足,AF=5,求CE的长.
分析 由DE⊥AC,BF⊥AC得到∠DEC=∠AFB=90°,由AB∥CD,得到∠C=∠A,根据三角形全等的判定定理即可证出Rt△DEC≌Rt△BFA,得到CE=AF.
解答 解:∵DE⊥AC,BF⊥AC,
∴∠DEC=∠AFB=90°,
∵AB∥CD,
在△DEC和△BFA中,
$\left\{\begin{array}{l}{∠DEC=∠AFC}\\{∠C=∠A}\\{DC=BA}\end{array}\right.$,
∴△DEC≌△BFA,
∴CE=AF,
CE=5.
点评 本题主要考查了全等三角形的性质和判定,平行线的性质等知识点,解此题的关键是证出△DEC≌△BFA.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列方程一定是一元二次方程的是( )
| A. | 2x2-1=3x | B. | 2x2-y=1 | C. | ax2+bx+c=0 | D. | 2x2+$\frac{1}{x}$=1 |
2.下列各式计算正确的是( )
| A. | 2(a+1)=2a+1 | B. | a3+a3=a6 | C. | -3a+2a=-a | D. | a2+a3=a5 |
3.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
| A. | 与x轴有两个交点 | B. | 顶点坐标是(1,-2) | ||
| C. | 与y轴的交点坐标是(0,3) | D. | 开口向上 |
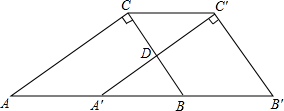 已知:如图,在Rt△ABC中.∠ACB=Rt∠,AC=4,BC=3.将△ABC沿AB方向平移至△A′B′C,使A′C′经过BC的中点D.
已知:如图,在Rt△ABC中.∠ACB=Rt∠,AC=4,BC=3.将△ABC沿AB方向平移至△A′B′C,使A′C′经过BC的中点D.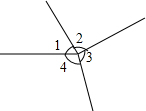 如图,∠1:∠2:∠3:∠4=3:4:5:6,求∠1、∠2、∠3、∠4的度数.
如图,∠1:∠2:∠3:∠4=3:4:5:6,求∠1、∠2、∠3、∠4的度数. 如图,C为线段AB上一点,D为线段BC的中点,AB=10cm,BC=acm,(5<a<10),求线段AC的长(用含a的式子表示).
如图,C为线段AB上一点,D为线段BC的中点,AB=10cm,BC=acm,(5<a<10),求线段AC的长(用含a的式子表示).