题目内容
1. 如图,在等边△ABC中,点D,E分別在边BC,AC上,DE∥AB,过点E作EF丄DE,交BC的延长线于点F.
如图,在等边△ABC中,点D,E分別在边BC,AC上,DE∥AB,过点E作EF丄DE,交BC的延长线于点F.(1)求∠F的度数;
(2)若CD=2,求DF、EF的长.
分析 (1)根据平行线的性质可得∠EDC=∠B=60°,根据三角形内角和定理即可求解;
(2)易证△EDC是等边三角形,再根据直角三角形的性质即可求解.
解答 解:(1)∵△ABC是等边三角形,
∴∠B=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°-∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形.
∴ED=DC=2,
∵∠DEF=90°,∠F=30°,
∴DF=2DE=4,
∴EF$\sqrt{3}$DE=2$\sqrt{3}$.
点评 本题考查了等边三角形的判定与性质,以及直角三角形的性质,熟记30度的锐角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
相关题目
13.如图,甲、乙、丙三个三角形中和△ABC全等的图形是( )


| A. | 甲和乙 | B. | 乙和丙 | C. | 只有乙 | D. | 只有丙 |
10.用一个平面去截一个圆锥,截面图形不可能是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,AF=DC,BC∥EF,若添加条件∠A=∠D,则可利用“ASA”说明△ABC≌△DEF.
如图,AF=DC,BC∥EF,若添加条件∠A=∠D,则可利用“ASA”说明△ABC≌△DEF. 如图,用四个形状、大小完全一样的长方形(长为b,宽为a),拼成一个大长方形中阴影部分的周长是4a+4b(用含a,b的式子表示).
如图,用四个形状、大小完全一样的长方形(长为b,宽为a),拼成一个大长方形中阴影部分的周长是4a+4b(用含a,b的式子表示).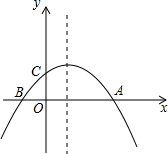 如图,已知抛物线y=-$\frac{1}{a}$(x+2)(x-a)(a>0)与x轴交于点A,B(点A在点B右侧),与y轴交于点C,抛物线过点N(6,一4).
如图,已知抛物线y=-$\frac{1}{a}$(x+2)(x-a)(a>0)与x轴交于点A,B(点A在点B右侧),与y轴交于点C,抛物线过点N(6,一4).