题目内容
6.已知⊙O的半径为5,且点O在直线l上,小明用一个三角板学具(∠ABC=90°,AB=BC=8)做数学实验:如图,若A、B两点在⊙O上滑动,直线BC分别与⊙O、l相交于点D、E.(1)求BD的长;
(2)当OE=6时,求BE的长.
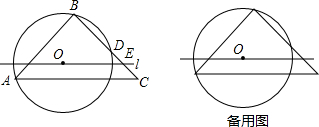
分析 (1)连接AD.根据90°圆周角所对的弦是直角可知AD是圆O的直径,在△ABD中,依据勾股定理可求得BD的长;
(2)连接OD,过点O作OF⊥BD,垂足为F.由垂径定理可求得FD、BF的长,然后在△FOE中,依据勾股定理可求得EF的长,从而可求得BE的长.
解答 解:(1)如图1所示:连接AD.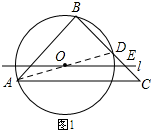
∵∠ABD=90°,
∴AD是圆O的直径.
∴AD=10.
在Rt△ABD中,BD=$\sqrt{A{D}^{2}-A{B}^{2}}$=6.
(2)如图2所示:连接OD,过点O作OF⊥BD,垂足为F.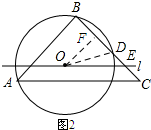
∵OF⊥BD,BD=6,
∴BF=FD=3.
在Rt△ODF中,OF=$\sqrt{O{D}^{2}-F{D}^{2}}$=4.
在Rt△OFE中,EF=$\sqrt{O{E}^{2}-O{F}^{2}}$=2$\sqrt{5}$.
∴BE=FB+EF=3+2$\sqrt{5}$.
点评 本题主要考查的是垂径定理、圆周角定理、勾股定理的应用,掌握此类问题的辅助线的作法是解题的关键.

练习册系列答案
相关题目
17.下列计算错误的是( )
| A. | $\sqrt{2}×\sqrt{5}=\sqrt{10}$ | B. | $\sqrt{2}+\sqrt{5}=\sqrt{7}$ | C. | $\sqrt{18}÷\sqrt{2}=3$ | D. | $\sqrt{12}=2\sqrt{3}$ |
1.下列计算正确的是( )
| A. | x3•x3=2x3 | B. | 4${\;}^{-2}=\frac{1}{16}$ | C. | $\sqrt{9}=±3$ | D. | (x3)2=x5 |
11.已知A(x1,y1)和B(x2,y2)是函数y=$\frac{{k}^{2}+1}{x}$图象上两点,当x1<x2时,y1与y2之间的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
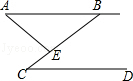 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为73°.
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为73°.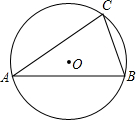 如图,△ABC内接于⊙O,∠BAC=30°,BC=$\sqrt{3}$,则⊙O的半径等于$\sqrt{3}$.
如图,△ABC内接于⊙O,∠BAC=30°,BC=$\sqrt{3}$,则⊙O的半径等于$\sqrt{3}$.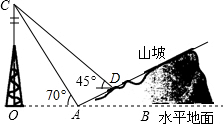 如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41)
如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41)