题目内容
6．先化简，再求值：（x-1-$\frac{3}{x+1}$）$÷\frac{{x}^{2}+4x+4}{x+1}$，其中x=$\frac{1}{3}$．分析 先根据分式混合运算的法则把原式进行化简，再把x的值代入进行计算即可．
解答 解：原式=$\frac{{x}^{2}-4}{x+1}$•$\frac{x+1}{（x+2）^{2}}$
=$\frac{（x+2）（x-2）}{x+1}$•$\frac{x+1}{{（x+2）}^{2}}$
=$\frac{x-2}{x+2}$，
当x=$\frac{1}{3}$时，原式=$\frac{\frac{1}{3}-2}{\frac{1}{3}+2}$=-$\frac{5}{7}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
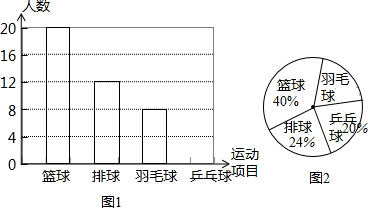
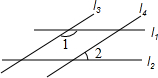如图：直线l1∥l2，l3∥l4，∠1比∠2的3倍少20°，则∠1=130°，∠2=50°．
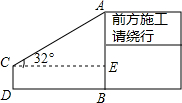如图，为了测量某交通路口设立的路况显示牌的立杆AB的高度，在D处用高1.2m的测角仪CD，测得最高点A的仰角为32°，已知观测点D到立杆AB的距离DB为3.8m，求立杆AB的高度．（结果精确到0.1m）
如图，在平面直角坐标系中，?ABCD的顶点A、B、C、D的坐标分别是（-5，0），（-2，0），（-3，2）．