题目内容
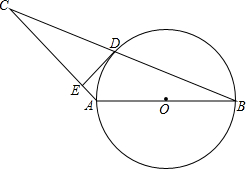 如图,在等腰△ABC中,AB=AC=5,BC=8,以一腰AB 为直径作⊙O交BC于D,又过D作DE⊥AC,垂足为E.
如图,在等腰△ABC中,AB=AC=5,BC=8,以一腰AB 为直径作⊙O交BC于D,又过D作DE⊥AC,垂足为E.(1)判断DE与圆O的位置关系,并说明理由;
(2)判断DE的长.
考点:切线的判定
专题:计算题
分析:(1)连结AD、OD,如图,根据圆周角定理,由AB为⊙O的直径得到∠ADB=90°,而AB=AC=5,则根据等腰三角形的性质得BD=CD=
BC=4,于是可判断OD为△ABC的中位线,所以OD∥AC,由于DE⊥AC,则OD⊥DE,然后根据切线的判定定理可得DE与圆O相切;
(2)在Rt△ABD中,根据勾股定理计算出AD=3,再证明Rt△ABD∽Rt△ADE,然后利用相似比即可计算出DE的长.
| 1 |
| 2 |
(2)在Rt△ABD中,根据勾股定理计算出AD=3,再证明Rt△ABD∽Rt△ADE,然后利用相似比即可计算出DE的长.
解答:解:(1)DE与圆O相切.理由如下:
 连结AD、OD,如图,
连结AD、OD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC=5,
∴BD=CD=
BC=4,
∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE与圆O相切;
(2)在Rt△ABD中,∵AB=5,BD=4,
∴AD=
=3,
∵AD为等腰△ABC的高,
∴AD平分∠BAC,
∴∠BAD=∠EAD,
∴Rt△ABD∽Rt△ADE,
∴
=
,即
=
,
∴DE=
.
 连结AD、OD,如图,
连结AD、OD,如图,∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC=5,
∴BD=CD=
| 1 |
| 2 |
∵OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE与圆O相切;
(2)在Rt△ABD中,∵AB=5,BD=4,
∴AD=
| AB2-BD2 |
∵AD为等腰△ABC的高,
∴AD平分∠BAC,
∴∠BAD=∠EAD,
∴Rt△ABD∽Rt△ADE,
∴
| BD |
| DE |
| AB |
| AD |
| 4 |
| DE |
| 5 |
| 3 |
∴DE=
| 12 |
| 5 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
与a2b是同类项的是( )
| A、22b |
| B、-3ab2 |
| C、-a2b |
| D、a2c |
下列事件是必然事件的是( )
| A、打开电视,正在播放广告 |
| B、某射击运动员射击一次,命中靶心 |
| C、抛掷一枚硬币,正面向上 |
| D、任意画一个三角形,它的内角和是180° |
直线m外的一点P,它到直线m上三点A,B,C的距离分别是6cm,3cm,5cm,则点P到直线m的距离为( )
| A、3cm | B、5cm |
| C、6cm | D、不大于3cm |
 如图,点C是线段AB的中点,BC=2BD,AB=4cm,求线段AD的长度.
如图,点C是线段AB的中点,BC=2BD,AB=4cm,求线段AD的长度.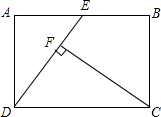 已知:如图,在矩形ABCD中,E是AB上的中点,CF⊥DE于F,若AD=8,AB=12.求CF的长.
已知:如图,在矩形ABCD中,E是AB上的中点,CF⊥DE于F,若AD=8,AB=12.求CF的长.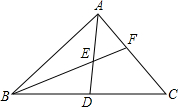 若D为△ABC边BC的中点,E为AD的中点,BE交AC于点F,则AF:FC=
若D为△ABC边BC的中点,E为AD的中点,BE交AC于点F,则AF:FC=