题目内容
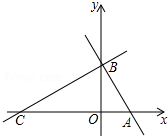如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB）且OA、OB的长分别是一元二次方程x2-（| 3 |
| 3 |
（1）求A、C两点的坐标；
（2）若点M从C点出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围．
考点：一次函数综合题
专题：
分析：（1）通过解一元二次方程x2-（
+1）x+
=0，求得方程的两个根，从而得到A、B两点的坐标，再根据两点之间的距离公式可求AB的长，根据AB：AC=1：2，可求AC的长，从而得到C点的坐标；
（2）分①当点M在CB边上时；②当点M在CB边的延长线上时；两种情况讨论可求S关于t的函数关系式．
| 3 |
| 3 |
（2）分①当点M在CB边上时；②当点M在CB边的延长线上时；两种情况讨论可求S关于t的函数关系式．
解答：解：（1）x2-（
+1）x+
=0，
（x-
）（x-1）=0，
解得x1=
，x2=1，
∵OA＜OB，
∴OA=1，OB=
，
∴A（1，0），B（0，
），
∴AB=2，
又∵AB：AC=1：2，
∴AC=4，
∴C（-3，0）；
（2）∵AB=2，AC=4，BC=2
，
∴AB2+BC2=AC2，
即∠ABC=90°，
由题意得：CM=t，CB=2
．
①当点M在CB边上时，S=2
-t（0≤t
）；
②当点M在CB边的延长线上时，S=t-2
（t＞2
）．
| 3 |
| 3 |
（x-
| 3 |
解得x1=
| 3 |
∵OA＜OB，
∴OA=1，OB=
| 3 |
∴A（1，0），B（0，
| 3 |
∴AB=2，
又∵AB：AC=1：2，
∴AC=4，
∴C（-3，0）；
（2）∵AB=2，AC=4，BC=2
| 3 |
∴AB2+BC2=AC2，
即∠ABC=90°，
由题意得：CM=t，CB=2
| 3 |
①当点M在CB边上时，S=2
| 3 |
| 3 |
②当点M在CB边的延长线上时，S=t-2
| 3 |
| 3 |
点评：考查了一次函数综合题，涉及的知识点有：解一元二次方程，两点之间的距离公式，函数思想，分类思想的运用，综合性较强，有一定的难度．
练习册系列答案
相关题目
在正方形ABCD中，P是BC边上与B、C不重合的任意点，DQ⊥AP于Q．证明：△DQA∽△ABP．
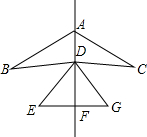如图是一个风筝的图案，它是以直线AF为对称轴的轴对称图形，下列结论中不一定成立的是（ ）| A、△ABD≌△ACD |
| B、AF垂直平分EG |
| C、∠B=∠C |
| D、DE=EG |
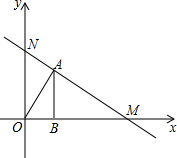如图，点M的坐标为（13，0），点A在第一象限，AB⊥x轴，垂足为B，tan∠AOB=