题目内容
14.计算(x-y)(-x-y)的结果是( )| A. | -x2+y2 | B. | -x2-y2 | C. | x2-y2 | D. | x2+y2 |
分析 本题是平方差公式的应用,-y是相同的项,互为相反项是-x与x,对照平方差公式计算.
解答 解:原式=(-y)2-x2
=y2-x2,
=-x2+y2,
故选A.
点评 本题考查了平方差公式的应用.运用平方差公式(a+b)(a-b)=a2-b2计算时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.

练习册系列答案
相关题目
5.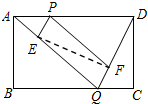 如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )
如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )
 如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )
如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )| A. | y=-$\frac{1}{3}$x2+x | B. | y=-$\frac{2}{3}$x2+2x | C. | y=-$\frac{1}{3}$x2+x+3 | D. | y=-$\frac{2}{3}$x2+2x+6 |
2. 观察下图的规律,在“?”处填上的数字是( )
观察下图的规律,在“?”处填上的数字是( )
 观察下图的规律,在“?”处填上的数字是( )
观察下图的规律,在“?”处填上的数字是( )| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
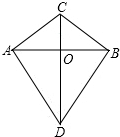 如图,CA=CB,DA=DB.求证:OA=OB,CD⊥AB.
如图,CA=CB,DA=DB.求证:OA=OB,CD⊥AB.