题目内容
13.关于x的一元二次方程x2-4x+k-3=0的两个实数根分别为x1,x2,且满足x1-7x2=0,试求出方程的两个实数根及k的值.分析 结合根与系数的关系以及x1-7x2=0,即可得出关于x1、x2的二元一次方程组,解方程组即可得出x1、x2的值,再利用根与系数的关系即可找出关于k的一元一次方程,解方程即可得出结论.
解答 解:由已知得:$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=4}\\{{x}_{1}-7{x}_{2}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=\frac{7}{2}}\\{{x}_{2}=\frac{1}{2}}\end{array}\right.$.
又∵x1•x2=k-3=$\frac{7}{2}$×$\frac{1}{2}$=$\frac{7}{4}$,
∴k=$\frac{19}{4}$.
答:方程的两个实数根分别为$\frac{7}{2}$、$\frac{1}{2}$,k的值为$\frac{19}{4}$.
点评 本题考查了根与系数的关系,根据根与系数的关系以及两根间的关系列出方程组是解题的关键.

练习册系列答案
相关题目
 如图,已知直线l1:y=3x+1和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
如图,已知直线l1:y=3x+1和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
 如图,正方形OABC顶点AC分别在x轴y轴正半轴上A(m,0)且m是分式方程$\frac{2}{x}$=$\frac{3}{x+1}$的解,OB=$\sqrt{2}$OA.
如图,正方形OABC顶点AC分别在x轴y轴正半轴上A(m,0)且m是分式方程$\frac{2}{x}$=$\frac{3}{x+1}$的解,OB=$\sqrt{2}$OA.
 如图1,直角三角形ABE,∠AEB=90°,∠BAE=30°,以AB为边作菱形ABCD,∠DAB=60°,点Q从A出发,沿折线AD-DC运动,运动到点C停止,设点Q运动的时间为t(s).△AEQ的面积s(cm2)与t(s)之间函数关系的图象由图2中的线段OP、PF给出.
如图1,直角三角形ABE,∠AEB=90°,∠BAE=30°,以AB为边作菱形ABCD,∠DAB=60°,点Q从A出发,沿折线AD-DC运动,运动到点C停止,设点Q运动的时间为t(s).△AEQ的面积s(cm2)与t(s)之间函数关系的图象由图2中的线段OP、PF给出.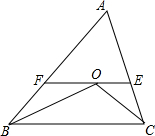 如图,△ABC中,BO,CO分别为∠ABC,∠ACB的平分线.交点为O,过O作EF平行于BC交AB,AC于F,E,探索BF+CE与FE的关系.说明理由.
如图,△ABC中,BO,CO分别为∠ABC,∠ACB的平分线.交点为O,过O作EF平行于BC交AB,AC于F,E,探索BF+CE与FE的关系.说明理由.