题目内容
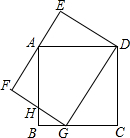 如图,G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.
如图,G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.(1)指出图中与△BHG相似的所有三角形;
(2)求FG的长.
考点:相似三角形的判定与性质
专题:
分析:(1)都是直角,其余两个角加起来为90°,根据对顶角、余角等关系,可以看出△AFH,△DCG,△DEA,△GBH均是相似三角形;
(2)根据
=
,可以求出FG,由ED=FG,只要求出
=
即可,根据相似三角形的性质即可求解.
(2)根据
| FG |
| CD |
| AD |
| GD |
| ED |
| CD |
| AD |
| GD |
解答:解:(1)△AFH,△DCG,△DEA,△GBH均是相似三角形;
(2)∵∠E=∠C=90°,∠EDA与∠CDG均为∠ADG的余角,
∴△DEA∽△DCG,
∴
=
,
∵ED=FG,
∴
=
,
由已知GD=5,AD=CD=4,
∴
=
,
即FG=
.
(2)∵∠E=∠C=90°,∠EDA与∠CDG均为∠ADG的余角,
∴△DEA∽△DCG,
∴
| FG |
| CD |
| AD |
| GD |
∵ED=FG,
∴
| ED |
| CD |
| AD |
| GD |
由已知GD=5,AD=CD=4,
∴
| FG |
| 4 |
| 4 |
| 5 |
即FG=
| 16 |
| 5 |
点评:本题考查了相似三角形的判定与性质,在做题过程中,要找全相似三角形要,综合考虑,解题的关键是掌握相似三角形判定和性质.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
某种蛋白质分子的直径为251000埃,已知1埃=10-10米,则用科学记数法表示该蛋白质分子的直径是( )
| A、2.51×105米 |
| B、2.51×104米 |
| C、2.51×10-6米 |
| D、2.51×10-5米 |
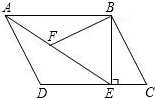 如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠AFB=∠D.
如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠AFB=∠D. 如图,AC∥BD∥EF,AC=20,BD=80,则EF=
如图,AC∥BD∥EF,AC=20,BD=80,则EF=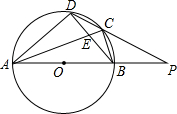 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.
如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.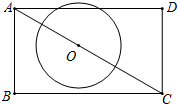 如图,已知矩形ABCD中,AB=2,BC=2
如图,已知矩形ABCD中,AB=2,BC=2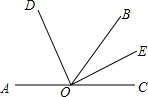 如图所示,∠AOB与∠BOC互为补角,OD平分∠AOB,OE平分∠BOC,求∠DOE的度数.
如图所示,∠AOB与∠BOC互为补角,OD平分∠AOB,OE平分∠BOC,求∠DOE的度数.