题目内容
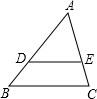 如图,已知AD•AC=AE•AB,求证:DE∥BC.
如图,已知AD•AC=AE•AB,求证:DE∥BC.考点:相似三角形的判定与性质
专题:证明题
分析:根据相似三角形判定推出△ADE∽△ABC,推出∠ADE=∠B,根据平行线的判定推出即可.
解答:证明:∵AD•AC=AE•AB,
∴
=
,
∵∠A=∠A,
∴△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.
∴
| AD |
| AB |
| AE |
| AC |
∵∠A=∠A,
∴△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.
点评:本题考查了相似三角形的性质和判定,平行线的判定的应用,注意:有两边的比相等,并且夹角也相等的两三角形相似.

练习册系列答案
相关题目
某种蛋白质分子的直径为251000埃,已知1埃=10-10米,则用科学记数法表示该蛋白质分子的直径是( )
| A、2.51×105米 |
| B、2.51×104米 |
| C、2.51×10-6米 |
| D、2.51×10-5米 |
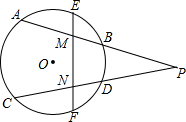 如图,已知圆O的弦AB、CD的延长线相交于点P,连接弧AB、弧CD的中点E、F分别交AB、CD于点M、N,求证:△PNM是等腰三角形.
如图,已知圆O的弦AB、CD的延长线相交于点P,连接弧AB、弧CD的中点E、F分别交AB、CD于点M、N,求证:△PNM是等腰三角形. 如图,点D是△ABC边AB上的一点,BD=2AD,P是△ABC外接圆上一点(点P在劣弧
如图,点D是△ABC边AB上的一点,BD=2AD,P是△ABC外接圆上一点(点P在劣弧
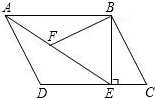 如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠AFB=∠D.
如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠AFB=∠D.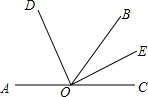 如图所示,∠AOB与∠BOC互为补角,OD平分∠AOB,OE平分∠BOC,求∠DOE的度数.
如图所示,∠AOB与∠BOC互为补角,OD平分∠AOB,OE平分∠BOC,求∠DOE的度数.