题目内容
12. 在矩形ABCD中,AD=4,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为E,EB=$\frac{1}{2}$OB,求AE的长.
在矩形ABCD中,AD=4,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为E,EB=$\frac{1}{2}$OB,求AE的长.
分析 由在矩形ABCD中,AE⊥BD于E,易证得△OAB是等边三角形,继而求得∠BAE的度数,由△OAB是等边三角形,求出∠ADE的度数,又由AD=4,即可求得AE的长.
解答 解:在矩形ABCD中,对角线AC与BD相交于点O,
∴AC=BD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,
∴OA=OB,
∵EB=$\frac{1}{2}$OB,AE⊥BD,
∴OA=AB 即OA=AB=OB,
∴△ABO是等边三角形.
即:∠ABO=60°
在矩形ABCD中,∠BAD=90°,
∴∠ADO=30°,
在Rt△AED中,∠AED=90°,∠ADO=30°,
∴AE=$\frac{1}{2}$AD=2.
点评 此题考查了矩形的性质、等边三角形的判定与性质以及含30°角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
17. 如图,长方形ABCD,点B表示的数为-2,点C在原点,CD=1,以点C为圆心,CA为半径画弧,交数轴于点P,则点P表示的实数是( )
如图,长方形ABCD,点B表示的数为-2,点C在原点,CD=1,以点C为圆心,CA为半径画弧,交数轴于点P,则点P表示的实数是( )
 如图,长方形ABCD,点B表示的数为-2,点C在原点,CD=1,以点C为圆心,CA为半径画弧,交数轴于点P,则点P表示的实数是( )
如图,长方形ABCD,点B表示的数为-2,点C在原点,CD=1,以点C为圆心,CA为半径画弧,交数轴于点P,则点P表示的实数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | -$\sqrt{3}$ |
1.下列各图,表示的数轴正确的是( )


| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
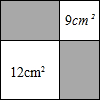 如图,从一个正方形中截取面积为9cm2或12cm2的两个小正方形,则留下阴影部分的面积为12$\sqrt{3}$cm2.
如图,从一个正方形中截取面积为9cm2或12cm2的两个小正方形,则留下阴影部分的面积为12$\sqrt{3}$cm2. 某游乐园门口需要修建一个由正方体和圆柱组合而成的一个立体图形,已知正方体的边长与圆柱的直径及高相等,都是0.8m.
某游乐园门口需要修建一个由正方体和圆柱组合而成的一个立体图形,已知正方体的边长与圆柱的直径及高相等,都是0.8m.