题目内容
3．在不透明的盒子中装有4个小球，一个黑球，一个蓝球，两个红球，从中摸取两个均为红球的概率为多少？（画树状图或列表）分析 画树状图展示所有12种等可能的结果数，再找出两个均为红球的结果数，然后根据概率公式求解．
解答 解：画树状图为：
共有12种等可能的结果数，其中两个均为红球的结果数为2，
所以摸取两个均为红球的概率=$\frac{2}{12}$=$\frac{1}{6}$．
点评 本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
已知y是关于x的函数，且x，y满足方程组$\left\{\begin{array}{l}{x+3y=4-a}\\{x-y=3a}\end{array}\right.$
14．5的相反数与-2的差是（ ）
| A． | 3 | B． | -3 | C． | 7 | D． | -7 |
8．
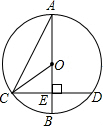如图，在⊙O中，直径AB与弦CD垂直相交于点E，连结AC，OC，若∠A=30°，OC=4，则弦CD的长是（ ）
如图，在⊙O中，直径AB与弦CD垂直相交于点E，连结AC，OC，若∠A=30°，OC=4，则弦CD的长是（ ）| A． | $2\sqrt{3}$ | B． | 4 | C． | $4\sqrt{3}$ | D． | 8 |
在矩形ABCD中，AD=4，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为E，EB=$\frac{1}{2}$OB，求AE的长．
13．若一次函数y=（k-1）x+1-k2经过原点，则k的值是（ ）
| A． | 1 | B． | ±1 | C． | -1 | D． | 任意实数 |