题目内容
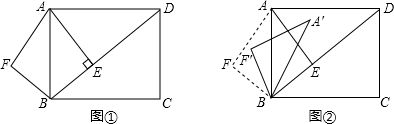
14.已知:如图①,在矩形ABCD中,AB=5,AD=$\frac{20}{3}$,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,平移中的△ABF为△A1B1F1设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).
①当点F分别平移到线段AB上时,求出m的值
②当点F分别平移到线段AD上时,当直接写出相应的m的值.
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AE交于点O,当∠A′BD=∠FAB时,请直接写出OB的长.
分析 (1)利用矩形性质、勾股定理及三角形面积公式求解;
(2)依题意画出图形,如答图2所示.利用平移性质,确定图形中的等腰三角形,分别求出m的值;
(3)在旋转过程中,分两种情形分别求解即可.
解答 解:(1)在Rt△ABD中,AB=5,AD=$\frac{20}{3}$,
由勾股定理得:BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{5}^{2}+(\frac{20}{3})^{2}}$=$\frac{25}{3}$.
∵S△ABD=$\frac{1}{2}$BD•AE=$\frac{1}{2}$AB•AD,
∴AE=$\frac{AB•AD}{BD}$=$\frac{5×\frac{20}{3}}{\frac{25}{3}}$=4.
在Rt△ABE中,AB=5,AE=4,由勾股定理得:BE=3.
(2)设平移中的三角形为△A′B′F′,如答图2所示:
由对称点性质可知,∠1=∠2.
由平移性质可知,AB∥A′B′,∠4=∠1,BF=B′F′=3.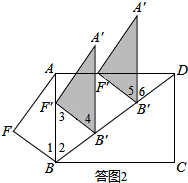
①当点F′落在AB上时,
∵AB∥A′B′,
∴∠3=∠4,
∴∠3=∠2,
∴BB′=B′F′=3,即m=3;
②当点F′落在AD上时,
∵AB∥A′B′,
∴∠6=∠2,
∵∠1=∠2,∠5=∠1,
∴∠5=∠6,
又易知A′B′⊥AD,
∴△B′F′D为等腰三角形,
∴B′D=B′F′=3,
∴BB′=BD-B′D=$\frac{25}{3}$-3=$\frac{16}{3}$,即m=$\frac{16}{3}$.
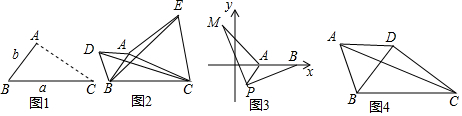
(3)如图3中,设AE交BA′于K.
∵∠KBE=∠FAB=∠BAE,∠KEB=∠AEB,
∴△EKB∽△EBA,
∴可得BE2=EK•EA,
∴EK=$\frac{9}{4}$,
在Rt△BEK中,BK=$\sqrt{B{E}^{2}+K{E}^{2}}$=$\sqrt{{3}^{2}+(\frac{9}{4})^{2}}$=$\frac{15}{4}$,
∴A′K=5-$\frac{15}{4}$=$\frac{5}{4}$,
∵∠A′=∠KBE,
∴OA′∥BE,
∴$\frac{OK}{KE}$=$\frac{A′K}{BK}$,
∴$\frac{OK}{\frac{9}{4}}$=$\frac{\frac{5}{4}}{\frac{15}{4}}$,
∴OK=$\frac{3}{4}$,
∴AO=AE-OK=KE=1.
如图4中,当∠DBA′=∠BAF时,点A′在线段BC上,
易证∠OAB=∠OBA,
∴OA=OB,设OA=OB=x,
在Rt△OBE中,∵OB2=OE2+BE2,
∴x2=32+(4-x)2,
∴x=$\frac{25}{8}$,
∴OA=$\frac{25}{8}$,
综上所述,满足条件的OA的长为1或$\frac{25}{8}$.
点评 本题是几何变换压轴题,涉及旋转与平移变换、矩形、勾股定理、等腰三角形等知识点.第(3)问难度很大,解题关键是画出各种旋转图形,依题意进行分类讨论;在计算过程中,注意识别旋转过程中的不变量,注意利用等腰三角形的性质简化计算.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 10%x=330 | B. | (1-10%)x=330 | C. | (1-10%)2x=330 | D. | (1+10%)x=330 |
| 甲车(辆) | 乙车(辆) | 荔枝(吨) | 香蕉(吨) | 合计(吨) |
| 1 | 1 | 6 | 3 | 9 |
| 2 | 4 | 16 | 10 | 36 |
| 3 | 6 | 24 | 15 | 39 |
| 4 | 9 | 34 | 22 | 56 |
(2)现计划将荔枝30吨,香蕉13吨运往外地,若租用甲、乙两种货车共10辆,求安排甲、乙两种货车有哪几种方案.
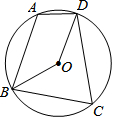 如图,四边形ABCD内接于⊙O,∠A=110°,则∠BOD=140°.
如图,四边形ABCD内接于⊙O,∠A=110°,则∠BOD=140°.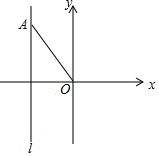 如图,在平面直角坐标系中,直线l平行于y轴,点A在直线l上,若点P是直线l上的一个动点,且使△PAO是以OA为腰的等腰三角形,则符合条件的点P有( )
如图,在平面直角坐标系中,直线l平行于y轴,点A在直线l上,若点P是直线l上的一个动点,且使△PAO是以OA为腰的等腰三角形,则符合条件的点P有( )