题目内容
3.下列命题中,是真命题的有( )①若a>b,则ac>bc;
②$\sqrt{25}$的平方根是±5;
③函数y=x2+$\frac{1}{\sqrt{-x}}$图象上的点P(x,y)一定在第二象限;
④一组数据3,5,4,5,5,6,10的众数和中位数都是5.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分别利用不等式的性质以及平方根的定义各象限点的坐标特点以及众数、中位数的定义分析得出答案.
解答 解:①若a>b,则ac>bc(c>0),故此命题是假命题;
②$\sqrt{25}$=5的平方根是±$\sqrt{5}$,故此命题是假命题;
③利用函数y=x2+$\frac{1}{\sqrt{-x}}$图象上的点P(x,y),可得x<0,y>0,故P点一定在第二象限,此命题是真命题;
④一组数据3,5,4,5,5,6,10的众数和中位数都是5,此命题是真命题.
故选:B.
点评 此题主要考查了命题与定理,熟练应用相关定义是解题关键.

练习册系列答案
相关题目
11.不等式组$\left\{\begin{array}{l}x+3>0\\ x-3≤0\end{array}\right.$的解集是( )
| A. | x>-3 | B. | x≤3 | C. | -3<x≤3 | D. | x≥3 |
8.不等式组$\left\{\begin{array}{l}\frac{x-3}{2}≥1\\ 8-x>0\end{array}\right.$的解集是( )
| A. | x≥5 | B. | 5≤x<8 | C. | x>8 | D. | 无解 |
13.一元二次方程x2+2x-5=0根的情况是( )
| A. | 无实数根 | B. | 有两个不相等的实数根 | ||
| C. | 只有一个实数根 | D. | 有两个相等的实数根 |
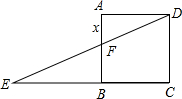 如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交A8于点F,AF=x(0.2≤x≤0.8),EC=y.则大致能反映y与x之闻函数关系的是y=$\frac{1}{x}$.
如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交A8于点F,AF=x(0.2≤x≤0.8),EC=y.则大致能反映y与x之闻函数关系的是y=$\frac{1}{x}$.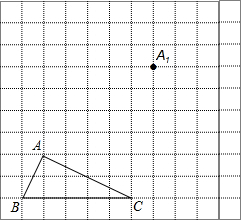 如图,在正方形网格中,△ABC为格点三角形(即三三角形的顶点都在格点上).
如图,在正方形网格中,△ABC为格点三角形(即三三角形的顶点都在格点上). 如图,四边形ABCD是矩形,点E是AD的中点,点F是BC的中点.求证:△ABF≌△CDE.
如图,四边形ABCD是矩形,点E是AD的中点,点F是BC的中点.求证:△ABF≌△CDE.