题目内容
1.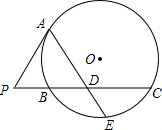 如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B、C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:
如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B、C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:(1)BE=EC;
(2)AD•DE=2PB2.
分析 (1)连接OE,OA,证明OE⊥BC,于是证得E是$\widehat{BC}$的中点,进而证得结论;
(2)利用切割线定理证得PD=2PB,PB=BD,然后根据相交弦定理即可得到结论.
解答 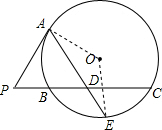 证明:(1)连接OA,OE,则∠OAE=∠OEA,∠OAP=90°,
证明:(1)连接OA,OE,则∠OAE=∠OEA,∠OAP=90°,
∵PC=2PA,D为PC的中点,
∴PA=PD,
∴∠PAD=∠CDE,
∴∠OEA+∠CDE=∠OAE+∠PAD=90°,
∴OE⊥BC,
∴E是$\widehat{BC}$的中点,
∴BE=EC;
(2)∵PA是⊙O的切线,
根据切割线定理得:PA2=PB•PC,
∵PC=2PA,
∴PA=2PB,
∴PD=2PB,
∴PB=DB,
∴BD•DC=PB•2PB,
根据相交弦定理得:BD•DC=AD•DE,
∴AD•DE=2PB2.
点评 本题考查了切线的性质,切割线定理,相交弦定理,垂径定理,正确的作出辅助线是解题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
11.不等式x<1在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
10.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{8}$ | C. | $\sqrt{12}$ | D. | $\sqrt{\frac{1}{2}}$ |
11. 如图,直线a,b相交于点O,若∠1等于40°,则∠2等于( )
如图,直线a,b相交于点O,若∠1等于40°,则∠2等于( )
 如图,直线a,b相交于点O,若∠1等于40°,则∠2等于( )
如图,直线a,b相交于点O,若∠1等于40°,则∠2等于( )| A. | 140° | B. | 120° | C. | 60° | D. | 50° |
 如图所示,BD=CE,添加一个条件,使∠ABE=∠ACD(利用“SSS”判定),并给予证明.
如图所示,BD=CE,添加一个条件,使∠ABE=∠ACD(利用“SSS”判定),并给予证明.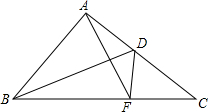 已知:在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,F为BC上一点,且∠ADB=∠CDF,连接AF.求证:AF⊥BD.
已知:在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,F为BC上一点,且∠ADB=∠CDF,连接AF.求证:AF⊥BD.