题目内容
如图①、②,解答下面各题:
(1)图①中,∠AOB=45°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数.
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
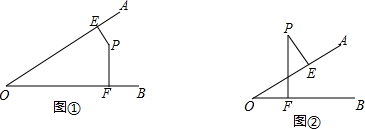
(1)图①中,∠AOB=45°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数.
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
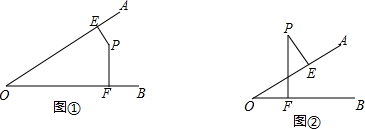
考点:多边形内角与外角,三角形内角和定理
专题:
分析:(1)利用四边形的内角和定理即可求解;
(2)利用垂直的定义和三角形的内角和定理求解;
(3)根据(1)和(2)的结果即可求解.
(2)利用垂直的定义和三角形的内角和定理求解;
(3)根据(1)和(2)的结果即可求解.
解答: 解:(1)∵PE⊥OA,PF⊥OB,
解:(1)∵PE⊥OA,PF⊥OB,
∴∠PEO=∠OFP=90°,
∴∠EPF=360°-90°-90°-45°=135°;
(2))∵PE⊥OA,PF⊥OB,
∴∠PEO=∠OFP=90°,
又∵∠OGF=∠PGE,
∴∠P=∠O;
(3)如果一个角的两边分别垂直于另一个角的两边,则这两个角相等或互补.
 解:(1)∵PE⊥OA,PF⊥OB,
解:(1)∵PE⊥OA,PF⊥OB,∴∠PEO=∠OFP=90°,
∴∠EPF=360°-90°-90°-45°=135°;
(2))∵PE⊥OA,PF⊥OB,
∴∠PEO=∠OFP=90°,
又∵∠OGF=∠PGE,
∴∠P=∠O;
(3)如果一个角的两边分别垂直于另一个角的两边,则这两个角相等或互补.
点评:考查了多边形内角与外角,三角形内角和定理.此题比较简单,只要结合多边形的内角和公式关系,正确理解内角和定理是关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,⊙O直径AB=8,∠CBD=30°,则CD=( )
如图,⊙O直径AB=8,∠CBD=30°,则CD=( )| A、4 | ||
| B、6 | ||
| C、3 | ||
D、2
|
比较-2.4,+(-0.5),-(-2),-|-3|的大小,下列正确的是( )
| A、-|-3|>-2.4>-(-2)>+(-0.5 ) |
| B、-(-2)>-|-3|>-2.4>+(-0.5) |
| C、-(-2)>+(-0.5)>-2.4>-|-3| |
| D、-|-3|>-(-2)>-2.4>+(-0.5) |
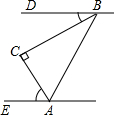 如图,在△ABC中,∠C=90°,若BD∥AE,∠CAE=70°,则∠DBC的度数是( )
如图,在△ABC中,∠C=90°,若BD∥AE,∠CAE=70°,则∠DBC的度数是( )| A、20° | B、40° |
| C、50° | D、70° |
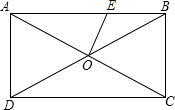 如图,矩形ABCD中,AC交BD于O,∠AOD=60°,OE⊥AC,AD=
如图,矩形ABCD中,AC交BD于O,∠AOD=60°,OE⊥AC,AD= 抛物线y=ax2-4ax+c交x轴于A、B两点,已知A(1,0),抛物线经过点N(4,-3),交y轴于点C.
抛物线y=ax2-4ax+c交x轴于A、B两点,已知A(1,0),抛物线经过点N(4,-3),交y轴于点C.