Question

12．已知△ABC和△AED都是等腰直角三角形，∠AED=∠ACB=90°，点B在AB上，连接BD、EC，点M、N分别为BD、EC的中点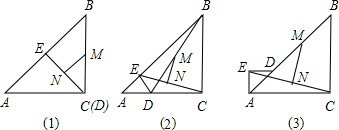

（1）当点E在AB上，且点C和点D重合时，如图（1）所示，则MN：EC=1：2；MN与EC的位置关系是（填“垂直”或“不垂直”）
（2）当点E、D分别在AB、AC上，且点C与点D不重合时，如图（2）．则（1）中MN与EC的位置关系还成立吗？请说明理由．
（3）在（2）的条件下，将Rt△AED绕点A逆时针旋转，使点D落在AB上，如图（3），则MN与EC的位置关系还成立吗？请说明理由．

Answer 1

分析 （1）根据三角形的中位线，可得答案；
（2）根据直角三角形斜边上的中线等于斜边的一半，可得EM=$\frac{1}{2}$BD，CM=$\frac{1}{2}$BD，根据等腰三角形的三线合一，可得答案；
（3）根据等腰直角三角形的性质，可得∠EDA=∠DAC=45°，根据平行线的判定与性质，可得∠DEN=∠GCN，根据全等三角形的判定与性质，可得DN与GN的关系，根据三角形的中位线，可得MN与BG的关系，根据全等三角形的判定与性质，可得∠ECA与∠GBC的关系，根据余角的性质，可得∠GBC与∠BCE的关系，垂直于平行线中的一条直线也垂直于另一条直线．

解答 解：（1）MN：EC=1：2，MN⊥EC，
故答案为：1：2；垂直；
（2）成立，连接EM、CM．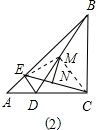
，
∵∠AED=∠ACB=90°，
∴∠BED=90°．
∵M是BD的中点，
∴EM=$\frac{1}{2}$BD，CM=$\frac{1}{2}$BD，
∴EM=CM．
∵N是EC的中点，
∴MN⊥EC；
（3）成立，理由如下：
连接DN并延长交AC于G，连接BG．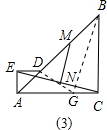
，
∵∠EDA=∠DAC=45°，
∴ED∥AC，
∴∠DEN=∠GCN．
∵N是EC的中点，
∴EN=CN．
在△EDN和△CGN中，
$\left\{\begin{array}{l}{∠DEN=∠GCN}\\{EN=CN}\\{∠DNE=∠GNC（对顶角相等）}\end{array}\right.$，
∴△EDN≌△CGN（ASA），
∴DN=GN．
∵M是BD的中点，
∴MN是△GDB的中位线，
∴MN∥BG．
在△ACE和△CBG中，
$\left\{\begin{array}{l}{AC=CB}\\{∠EAC=∠GCB}\\{AE=CG}\end{array}\right.$，
∴△ACE≌△CBG（SAS），
∴∠ECA=∠GBC．
∵∠ECA+∠BCE=90°，
∴∠GBC+∠BCE=90°，
∴BG⊥EC，即MN⊥EC．

点评 本题考查了全等三角形的判定，（1）利用了三角形的中位线定理，（2）利用了直角三角形的性质，等腰三角形的性质，（3）利用了全等三角形的判定与性质，三角形中位线的性质，余角的性质，垂线的判定．