题目内容
20.已知关于x的方程x2-4x-2m+8=0.(1)当m为何值时,方程有两个不相等的实数根;
(2)试写出m的一个数值,使方程的两个实数根一个大于0,另一个小于0.
分析 (1)要使方程有两个不相等的实数根,只需根的判别式大于0即可;
(2)根据根与系数的关系,要使方程的两个实数根一个大于0,另一个小于0,只需两根之积小于0即可.
解答 解:(1)当△=(-4)2-4×1×(-2m+8)>0即m>2时,方程有两个不相等的实数根;
(2)根据根与系数的关系可得:
当△≥0且-2m+8<0即m>4时,方程的两个实数根一个大于0,另一个小于0.
故m为大于4的任意一个实数,如5,6,…
点评 本题主要考查了根的判别式、根与系数的关系等知识,需要注意的是运用根与系数的关系时,首先要保证根的判别式非负.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
15.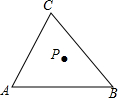 如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
 如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
如图所示,A,B,C分别表示三个村庄,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )| A. | ∠A,∠B的平分线的交点处 | |
| B. | AB的垂直平分线与∠B的平分线的交点处 | |
| C. | BC的垂直平分线与∠A的平分线的交点处 | |
| D. | AB,BC的垂直平分线的交点处 |
7. 如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
 如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )
如图,已知二次函数y=x2+bx+3的图象与x轴正半轴交于B、C两点,BC=2,则b的值为( )| A. | 4 | B. | -4 | C. | ±4 | D. | -5 |
 如图,在△ABC中,∠BAC的平分线与∠ABC外角的平分线交于点F,∠ABC的平分线与AF交于点D,若∠C=80°,求∠F的度数.
如图,在△ABC中,∠BAC的平分线与∠ABC外角的平分线交于点F,∠ABC的平分线与AF交于点D,若∠C=80°,求∠F的度数.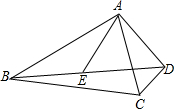 如图,已知:∠ACB=∠ADE,∠ABC=∠AED,求证:△ABE∽△ACD.
如图,已知:∠ACB=∠ADE,∠ABC=∠AED,求证:△ABE∽△ACD.