题目内容
15.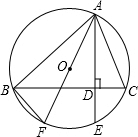 如图,△ABC内接于⊙O,AE⊥BC于D,交⊙O于E,AF为⊙O的直径.
如图,△ABC内接于⊙O,AE⊥BC于D,交⊙O于E,AF为⊙O的直径.(1)求证:∠BAF=∠CAE;
(2)求证:AB•AC=AD•AF;
(3)若过O作0N⊥AB于N,则ON与CE之间有何数量关系?
分析 (1)由等弧所对的圆周角相等可知∠AFB=∠ACB,然后由∠ABF=∠ADC,可证明∠BAF=∠CAE;
(2)由∠ABF=∠ADC,∠AFB=∠ACB可知△ABF∽△ADC,由相似三角形的性质可知AB•AC=AD•AF;
(3)由∠BAF=∠CAE,可知BF=CE,然后证明ON是△ABF的中位线,从而得到ON=$\frac{1}{2}BF$,于是可得到ON=$\frac{1}{2}EC$.
解答 解:(1)∵AF是⊙O的直径,
∴∠ABF=90°.
∴∠BAF+∠BFA=90°.
∵AE⊥BC,
∴∠ADC=90°.
∴∠DAC+∠C=90°.
∵∠F=∠C,
∴∠BAF=∠CAE.
(2)∵∠ABF=∠ADC=90°,∠F=∠C,
∴△ABF∽△ADC.
∴$\frac{AB}{AD}=\frac{AF}{AC}$.
∴AB•AC=AD•AF.
(3)如图所示: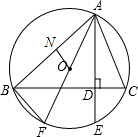
∵ON⊥AB,
∴AN=BN.
又∵OA=0F,
∴ON是△ABF的中位线.
∴ON=$\frac{1}{2}BF$.
∵∠BAF=∠CAE,
∴BF=EC.
∴ON=$\frac{1}{2}EC$.
点评 本题主要考查的是圆周角定理、相似三角形的性质和判定、三角形中位线的性质,证得ON是△ABF的中位线是解题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
5.如果3x=2y(x、y均不为零),那么x:y的值是( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
6.抛物线y=ax2+4ax-5的对称轴为( )
| A. | x=-2a | B. | x=4 | C. | x=2a | D. | x=-2 |
4. 如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )
如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )
 如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )
如图,矩形ABCD中,点B的坐标是(4,3),直线l平行于对角线AC,直线l从原点出发,沿x轴的正方向以每秒1个单位长度运动,与矩形OABC的两边分别交于点M,N,当MN=$\frac{1}{2}$AC时,直线l运动的时间是( )| A. | 2秒 | B. | 6秒 | C. | 2秒或6秒 | D. | 4秒或8秒 |
18.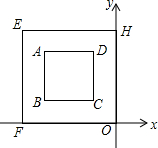 如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )
如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )
 如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )
如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )| A. | (-2,2) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | (-4,4) | D. | (0,0) |
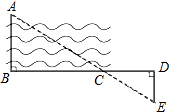 如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是多少?
如图所示,要测量河两岸相对的两点A,B的距离,先从B处出发与AB成90°角方向,向前走80米到C处立一标杆,然后方向不变向前走50米至D处,在D处转90°,沿DE方向走30米,到E处,使A(目标物),C(标杆)与E在同一条直线上,那么可测得A,B间的距离是多少?