题目内容
(1)解方程:
+
=
;
(2)解不等式组:
.
| x |
| x+2 |
| x+2 |
| 2-x |
| 8 |
| x2-4 |
(2)解不等式组:
|
考点:解分式方程,解一元一次不等式组
专题:计算题
分析:(1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解答:解:(1)去分母得:x(x-2)-(x+2)2=8,
整理得:x2-2x-x2-4x-4=8,
解得:x=-2,
经检验x=-2是增根,分式方程无解;
(2)
,
由①得:x≤2;
由②得:x>-1,
则不等式组的解集为-1<x≤2.
整理得:x2-2x-x2-4x-4=8,
解得:x=-2,
经检验x=-2是增根,分式方程无解;
(2)
|
由①得:x≤2;
由②得:x>-1,
则不等式组的解集为-1<x≤2.
点评:此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
若将函数y=3x2的图象向右平行移动1个单位,再向上平移5个单位,可得到的抛物线是( )
| A、y=3(x+1)2-5 |
| B、y=3(x+1)2+5 |
| C、y=3(x-1)2-5 |
| D、y=3(x-1)2+5 |
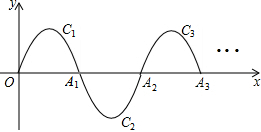 如图,一段抛物线:y=-x(x-4)(0≤x≤4),记为C1,它与x轴交于点O,A1:
如图,一段抛物线:y=-x(x-4)(0≤x≤4),记为C1,它与x轴交于点O,A1: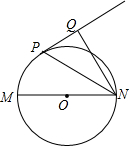 如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.
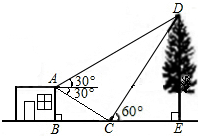 如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知平房高AB为4米,且B、C、E三点在同一条直线上,请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计).
如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知平房高AB为4米,且B、C、E三点在同一条直线上,请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计).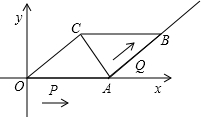 已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从0点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从0点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒. (1)计算:2
(1)计算:2