题目内容
已知:如图,Rt△ABC中,∠ACB=90°°,AC=3,BC=4.
(1)求AB的长;
(2)在直线AC、BC上分别取一点M、N,使得△AMN≌△ABN,求CN的长.

考点: 勾股定理;全等三角形的判定.
分析: (1)由勾股定理求出AB即可;
(2)分两种情况:①当∠BAN=∠MAN,且AM=AB时,则BN=MN,且AM=AB=5,求出CM,设CN=x,在Rt△MCN中,由勾股定理得出方程,解方程即可;
②当∠BAN=∠MAN,且AM=AB时,则BN=MN,且AM=AB=5,求出CM=8,设CN=x,则BN=MN=x+4,在Rt△MCN中,由勾股定理得出方程,解方程即可.
解答: 解:(1)∵∠ACB=90°,AC=3,BC=4,
∴AB=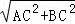 =
=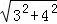 =5;
=5;
(2)分两种情况:
①如图1所示:
当∠BAN=∠MAN,且AM=AB时,有△AMN≌△ABN,
则BN=MN,且AM=AB=5,
∴CM=2,
设CN=x,
在Rt△MCN中,MC2+CN2=MN2,
即22+x2=(4﹣x)2,
解得:x=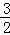 ,
,
∴CN=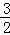 ;
;
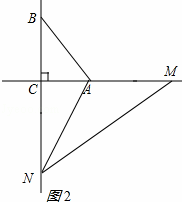
②如图2所示:
当∠BAN=∠MAN,且AM=AB时,有△AMN≌△ABN,
则BN=MN,且AM=AB=5,
∴CM=8,
设CN=x,则BN=MN=x+4,
在Rt△MCN中,MC2+CN2=MN2,
即82+x2=(4+x)2,
解得:x=6,
∴CN=6;
综上所述:CN的长为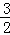 或6.
或6.
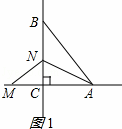

练习册系列答案
相关题目
 =
= 

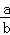 =﹣1; ④若
=﹣1; ④若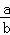 =﹣1,则a、b互为相反数.其中正确的结论有( )
=﹣1,则a、b互为相反数.其中正确的结论有( ) C. 3 D. ±3
C. 3 D. ±3