题目内容
17. 反比例函数y=$\frac{k}{x}$的图象如图所示,下列说法正确的是( )
反比例函数y=$\frac{k}{x}$的图象如图所示,下列说法正确的是( )| A. | 常数k<-1 | |
| B. | 在每个象限内,y随x的增大而增大 | |
| C. | 若P(x,y)在图象上,则P′(-x,-y)也在图象上 | |
| D. | 若A(-1,m),B(2,n)在图象上,则m>n |
分析 结合函数图象逐一分析四个选项的对错,由此即可得出结论.
解答 解:A、∵反比例函数y=$\frac{k}{x}$的图象在第一三象限,
∴k>0,
∴A错误;
B、根据函数图象可得出:在每个象限内,y随x的增大而减小,
∴B错误;
C、由反比例函数的对称性可知:
若P(x,y)在图象上,则P′(-x,-y)也在图象上,
∴C正确;
D、根据函数图象可得出:在第三象限内,y<0,在第一象限内,y>0,
∵A(-1,m),B(2,n),
∴m<0<n,
∴D错误.
故选C.
点评 本题考查了反比例函数的性质,解题的关键是结合反比例函数的性质以及函数图象逐一分析四个选项.本题属于基础题,难度不大,解决该题型题目时,熟悉掌握反比例函数图象的有关知识是关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
10.平行四边形的一边是10cm,那么这个平行四边形的两条对角线的长不可能是( )
| A. | 14cm和6cm | B. | 16cm和8cm | C. | 18cm和10cm | D. | 10cm和12cm |
8.若-$\frac{1}{3}$axb与2ab1-y的和是一个单项式,则x-y2016的值为( )
| A. | 1 | B. | -3 | C. | -1 | D. | 0 |
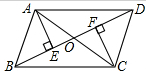 如图,在平行四边形ABCD中,对角线AC.BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:OE=OF.
如图,在平行四边形ABCD中,对角线AC.BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:OE=OF. 如图,已知点A(m,m+1),B(m+3,m-1)
如图,已知点A(m,m+1),B(m+3,m-1) 如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转99次后顶点A在整个旋转过程中所经过的路程之和是( )
如图,在矩形ABCD中,已知AB=8,BC=6,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转99次后顶点A在整个旋转过程中所经过的路程之和是( ) 在我市十个全覆盖工作的推动下,某乡镇准备在相距3千米的A、B两个工厂间修一条笔直的公路,在工厂A北偏东60°方向、工厂北偏西45°方向有一点P,以P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据:$\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$)
在我市十个全覆盖工作的推动下,某乡镇准备在相距3千米的A、B两个工厂间修一条笔直的公路,在工厂A北偏东60°方向、工厂北偏西45°方向有一点P,以P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据:$\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$) 如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF
如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF 的对称轴是直线( )
的对称轴是直线( )