题目内容
6. 如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF
如图,DE是△ABC的中位线,延长DE到F,使EF=DE,连接BF(1)求证:BF=DC;
(2)求证:四边形ABFD是平行四边形.
分析 (1)连接DB,CF,利用对角线互相平分的四边形是平行四边形可得四边形CDBF是平行四边形,进而可得CD=BF;
(2)由(1)可得CD∥FB,再利用三角形中位线定理可得DF∥AB,根据两组对边分别平行的四边形是平行四边形可得结论.
解答 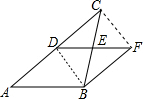 证明:(1)连接DB,CF,
证明:(1)连接DB,CF,
∵DE是△ABC的中位线,
∴CE=BE,
∵EF=ED,
∴四边形CDBF是平行四边形,
∴CD=BF;
(2)∵四边形CDBF是平行四边形,
∴CD∥FB,
∴AD∥BF,
∵DE是△ABC的中位线,
∴DE∥AB,
∴DF∥AB,
∴四边形ABFD是平行四边形.
点评 此题主要考查了平行四边形的判定和性质,以及三角形中位线定理,关键是掌握对角线互相平分的四边形是平行四边形,两组对边分别平行的四边形是平行四边形.

练习册系列答案
相关题目
16.在?ABCD中,AC与BD相交于点O,要使四边形ABCD是菱形,还需添加一个条件,这个条件可以是( )
| A. | AO=CO | B. | AO=BO | C. | AO⊥BO | D. | AB⊥BC |
17. 反比例函数y=$\frac{k}{x}$的图象如图所示,下列说法正确的是( )
反比例函数y=$\frac{k}{x}$的图象如图所示,下列说法正确的是( )
 反比例函数y=$\frac{k}{x}$的图象如图所示,下列说法正确的是( )
反比例函数y=$\frac{k}{x}$的图象如图所示,下列说法正确的是( )| A. | 常数k<-1 | |
| B. | 在每个象限内,y随x的增大而增大 | |
| C. | 若P(x,y)在图象上,则P′(-x,-y)也在图象上 | |
| D. | 若A(-1,m),B(2,n)在图象上,则m>n |