题目内容
8.若a,b满足a=$\sqrt{b-2}$+$\sqrt{2-b}$+7,求ab的值.分析 根据被开方数是非负数,可得不等式组,根据解不等式组,可得a、b的值,根据乘方的意义,可得答案.
解答 解:由a=$\sqrt{b-2}$+$\sqrt{2-b}$+7,得
$\left\{\begin{array}{l}{b-2≥0}\\{2-b≥0}\\{a=7}\end{array}\right.$,
解得a=7,b=2.
ab=72=49.
点评 本题考查了二次根式有意义的条件,利用被开方数是非负数得出不等式组是解题关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
17.已知3×3a=315,则a的值为( )
| A. | 5 | B. | 13 | C. | 14 | D. | 15 |
18.若P,Q是直线AB外不重合的两点,则下列说法不正确的是( )
| A. | 直线PQ可能与直线AB垂直 | |
| B. | 直线PQ可能与直线AB平行 | |
| C. | 过点P的直线一定能与直线AB相交 | |
| D. | 过点Q只能画出一条直线与直线AB平行 |
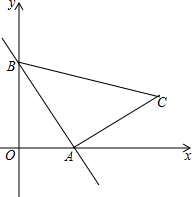 如图,在平面直角坐标系中,点C的坐标为(3,1),动点A以每秒1个单位的速度从点O出发沿x轴正半轴运动,同时动点B以每秒2个单位的速度从点O出发沿y轴正半轴运动,作直线AB.设运动的时间为t秒,是否存在t,使△ABC是等腰三角形?若存在,求t的值;若不存在,请说明理由.
如图,在平面直角坐标系中,点C的坐标为(3,1),动点A以每秒1个单位的速度从点O出发沿x轴正半轴运动,同时动点B以每秒2个单位的速度从点O出发沿y轴正半轴运动,作直线AB.设运动的时间为t秒,是否存在t,使△ABC是等腰三角形?若存在,求t的值;若不存在,请说明理由. 在正方形ABCD中,点F是对角线AC上任意一点,EF⊥BF交边AD于点E,联结BE.求∠EBF.
在正方形ABCD中,点F是对角线AC上任意一点,EF⊥BF交边AD于点E,联结BE.求∠EBF.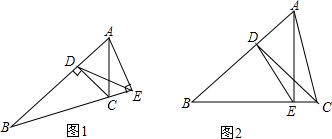
 如图,在直角坐标系中,⊙M经过原点O,且与x轴、y轴分别交于A(-6,0)、B(0,-8).
如图,在直角坐标系中,⊙M经过原点O,且与x轴、y轴分别交于A(-6,0)、B(0,-8).