题目内容
11. 如图,∠B=46°,∠D=42°,∠DAB和∠BCD的平分线AP和CP相交于点P,则∠P=45°.
如图,∠B=46°,∠D=42°,∠DAB和∠BCD的平分线AP和CP相交于点P,则∠P=45°.
分析 先根据角平分线定义得到∠1=∠2,∠3=∠4,再利用三角形内角和定理和对顶角相等得到∠1+∠D=∠4+∠P①,∠1+∠2+∠D=∠3+∠4+∠B,即2∠1+∠D=2∠4+∠B②,然后利用①×2-②得∠P=$\frac{1}{2}$(∠D+∠B),再把∠B=46°,∠D=42°代入计算即可.
解答 解: ∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠1=∠2,∠3=∠4,
∵∠1+∠D=∠4+∠P①,
∠1+∠2+∠D=∠3+∠4+∠B,即2∠1+∠D=2∠4+∠B②,
由①×2-②得∠D=2∠P-∠B,
∴∠P=$\frac{1}{2}$(∠D+∠B)=$\frac{1}{2}$×(46°+42°)=45°.
故答案为45°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.解答的关键是找准相关的三角形,然后利用三角形内角和定理建立等量关系.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图,在?ABEF中,AB=2,AF<AB.现将线段EF在直线EF上移动,在移动过程中,设线段EF的对应线段为CD,连接AD、BC.
如图,在?ABEF中,AB=2,AF<AB.现将线段EF在直线EF上移动,在移动过程中,设线段EF的对应线段为CD,连接AD、BC.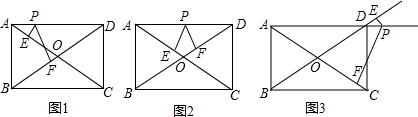
 如图,直线a∥b,直线c与直线a、b都相交,∠1=115°,则∠2=65°.
如图,直线a∥b,直线c与直线a、b都相交,∠1=115°,则∠2=65°.