题目内容
如果x2-4x+y2+6y+
+13=0,则x-z+y的平方根是 .
| z+2 |
考点:配方法的应用,非负数的性质:偶次方,平方根,非负数的性质:算术平方根
专题:
分析:首先配方,然后运用非负数的性质求出x、y、z的值,问题即可解决.
解答:解:∵x2-4x+y2+6y+
+13=0,
∴(x-2)2+(y+3)2+
=0,
又∵(x-2)2≥0,(y+3)2≥0,
≥0,
∴x-2=0,y+3=0,z+2=0,
∴x=2,y=-3,z=-2;
∴x-z+y=1,x-z+y的平方根是±1.
故该题答案为±1.
| z+2 |
∴(x-2)2+(y+3)2+
| z+2 |
又∵(x-2)2≥0,(y+3)2≥0,
| z+2 |
∴x-2=0,y+3=0,z+2=0,
∴x=2,y=-3,z=-2;
∴x-z+y=1,x-z+y的平方根是±1.
故该题答案为±1.
点评:该题主要考查了配方法、非负数的性质、平方根的定义及其应用问题;解题的关键是正确配方,准确化简、求值.

练习册系列答案
相关题目
根据下表的对应值,试判断一元二次方程ax2+bx+c=0的一解的取值范围是( )
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.07 |
| A、3<x<3.23 |
| B、3.23<x<3.24 |
| C、3.24<x<3.25 |
| D、3.25<x<3.26 |
若函数y=(k-1)x+k2-1是正比例函数,则k的值是( )
| A、-1 | B、1 |
| C、-1或1 | D、任意实数 |
 一座圆弧形拱桥如图,圆弧形桥拱的跨度AB=12米,C为桥拱的中点,拱高CD=4米,求拱桥的半径.
一座圆弧形拱桥如图,圆弧形桥拱的跨度AB=12米,C为桥拱的中点,拱高CD=4米,求拱桥的半径. 已知一次函数y=-kx+k的图象如图,则二次函数y=-kx2-2x+k的图象大致是( )
已知一次函数y=-kx+k的图象如图,则二次函数y=-kx2-2x+k的图象大致是( )




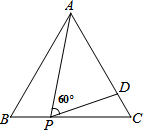 如图,等边三角形△ABC的边长为3,点P为BC上的一点,且PC=2,点D为AC上的一点,若∠APD=60°,则CD的长为
如图,等边三角形△ABC的边长为3,点P为BC上的一点,且PC=2,点D为AC上的一点,若∠APD=60°,则CD的长为