题目内容
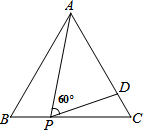 如图,等边三角形△ABC的边长为3,点P为BC上的一点,且PC=2,点D为AC上的一点,若∠APD=60°,则CD的长为
如图,等边三角形△ABC的边长为3,点P为BC上的一点,且PC=2,点D为AC上的一点,若∠APD=60°,则CD的长为考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:由条件可得到∠BAP=∠DPC,且∠B=∠C,可证得△ABP∽△PCD,可得
=
,代入可求得CD的长.
| AB |
| PC |
| BP |
| CD |
解答:解:
∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵∠APD=60°,
∴∠BAP+∠APB=∠APB+∠DPC=120°,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴
=
,
又AB=BC=3,PC=2,可得BP=1,
∴
=
,
解得CD=
,
故答案为:
.
∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵∠APD=60°,
∴∠BAP+∠APB=∠APB+∠DPC=120°,
∴∠BAP=∠DPC,
∴△ABP∽△PCD,
∴
| AB |
| PC |
| BP |
| CD |
又AB=BC=3,PC=2,可得BP=1,
∴
| 3 |
| 2 |
| 1 |
| CD |
解得CD=
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题主要考查相似三角形的判定和性质及等边三角形的性质,由条件得到∠BAP=∠DPC证得△ABP∽△PCD是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
数轴上的点P到原点的距离为3,点P表示的有理数是( )
| A、3 | B、-3 | C、6 | D、3或-3 |
下列各式中,完全平方公式应用正确的是( )
| A、(2a+3b)2=2a2+12ab+3b2 |
| B、(-x+y)2=-x2+2xy+y2 |
| C、(3a-4b)2=9a2-12ab+16b2 |
| D、(mn-4)2=m2n2-8mn+16 |
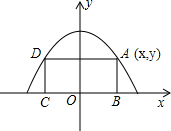 如图,矩形ABCD的顶点B,C在x轴上,A,D在抛物线y=-
如图,矩形ABCD的顶点B,C在x轴上,A,D在抛物线y=-