题目内容
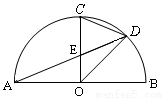
15.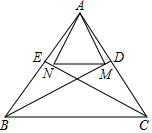 如图,已知:AB=AC,BD、CE分别是∠B、∠C的平分线,AM⊥BD于点M,AN⊥CE于点N.说明△AMN是等腰三角形的理由.
如图,已知:AB=AC,BD、CE分别是∠B、∠C的平分线,AM⊥BD于点M,AN⊥CE于点N.说明△AMN是等腰三角形的理由.
分析 先根据等腰三角形的性质以及角平分线的定义,得出△AMB≌△ANC(AAS),进而得到AM﹦AN,即△AMN是等腰三角形.
解答 证明:∵AB﹦AC(已知),
∴∠ABC﹦∠ACB(等边对等角).
∵BD、CE分别平分∠ABC、∠ACB(已知),
∴∠ABD﹦∠ACE.
∵AM⊥BD,AN⊥CE(已知),
∴∠AMB﹦∠ANC﹦90°(垂直的定义).
∴在△AMB和△ANC中,
$\left\{\begin{array}{l}{∠AMB﹦∠ANC}\\{∠ABD﹦∠ACE}\\{AB﹦AC}\end{array}\right.$,
∴△AMB≌△ANC(AAS),
∴AM﹦AN,
∴△AMN是等腰三角形.
点评 本题考查了全等三角形的判定与性质及等腰三角形的性质与判定,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
20.若有理数a、b满足|a+3|+(b-2)2=0,则代数式ab的值为( )
| A. | -6 | B. | 6 | C. | -9 | D. | 9 |
7.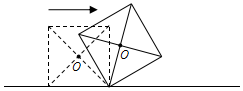 如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )
如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )
 如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )
如图,边长为a的正方形木块在水平地面上沿直线滚动一周(没有滑动),则它的中心点O所经过的路径长为( )| A. | 4a | B. | 2$\sqrt{2}$πa | C. | $\sqrt{2}$πa | D. | $\sqrt{2}$a |
4.要反映杭州市一天内气温的变化情况宜采用( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 频数分布直方图 |
 如图,数轴上点A、B、C所对应的数分别为a、b、c,化简|a|+|c-b|-|a+b-c|=0.
如图,数轴上点A、B、C所对应的数分别为a、b、c,化简|a|+|c-b|-|a+b-c|=0.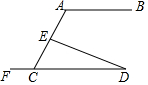 如图,AB∥CD,DE交AC于点E,下列结论:①∠A=∠ACF;②∠A=∠CED;③∠A+∠AED=180°;④∠AED>∠DCE;其中正确的个数是( )
如图,AB∥CD,DE交AC于点E,下列结论:①∠A=∠ACF;②∠A=∠CED;③∠A+∠AED=180°;④∠AED>∠DCE;其中正确的个数是( )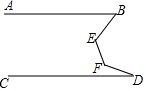 如图,AB∥CD,∠B=42°,∠D=17°,求∠E+∠F的度数.
如图,AB∥CD,∠B=42°,∠D=17°,求∠E+∠F的度数.