题目内容
20．若有理数a、b满足|a+3|+（b-2）2=0，则代数式ab的值为（ ）| A． | -6 | B． | 6 | C． | -9 | D． | 9 |
分析 依据非负数的性质可求得a，b的值，然后可代入计算即可．
解答 解：∵有理数a、b满足|a+3|+（b-2）2=0，
∴a=-3，b=2．
∴ab=（-3）2=9．
故选：D．
点评 本题主要考查的是非负数的性质，求得代数式的值，求得a，b的值是解题的关键．
练习册系列答案
相关题目
10．下列各组数中，互为倒数的是（ ）
| A． | 2与-2 | B． | -$\frac{2}{3}$与$\frac{3}{2}$ | C． | -1与（-1）2016 | D． | -$\frac{3}{4}$与-$\frac{4}{3}$ |
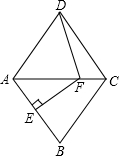如图，在菱形ABCD中，AB的垂直平分线EF交对角线AC于点F，垂足为点E，连接DF，且∠CDF=27°，则∠DAF等于51度．
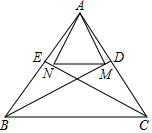如图，已知：AB=AC，BD、CE分别是∠B、∠C的平分线，AM⊥BD于点M，AN⊥CE于点N．说明△AMN是等腰三角形的理由．
5．下列四个关系式中，y是x的反比例函数的是（ ）
| A． | y=4x | B． | y=$\frac{1}{3x}$ | C． | y=$\frac{1}{{x}^{2}}$ | D． | y=$\frac{1}{x+1}$ |
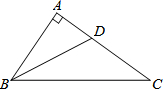如图，在Rt△ABC中，∠A=90°，∠ABC的平分线BD交AC于点D，AB=6，BC=10，则AD为3．
9．已知P=m2-2m，Q=2m-4，则P，Q的大小关系为（ ）
| A． | P≥Q | B． | P＞Q | C． | P≤Q | D． | P＜Q |
B. 
C. 
D. 