题目内容
已知O为直线AB上的一点,∠EOF为直角,OC平分∠BOE.
(1)如图1,若∠AOE=46°,则∠COF= 度;
(2)如图1,若∠AOE=n°(0<n<90),求∠COF的度数;(用含n的式子表示)
(3)如图2,若∠AOE=n°(90<n<180),OD平分∠AOC,且∠AOD-∠BOF=15°,求n的值.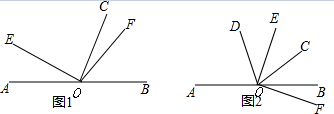
(1)如图1,若∠AOE=46°,则∠COF=
(2)如图1,若∠AOE=n°(0<n<90),求∠COF的度数;(用含n的式子表示)
(3)如图2,若∠AOE=n°(90<n<180),OD平分∠AOC,且∠AOD-∠BOF=15°,求n的值.
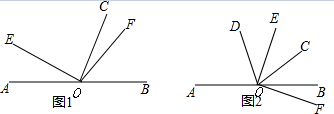
考点:角的计算,角平分线的定义
专题:
分析:(1)由∠AOE=46°,可以求得∠BOE=134°,再由OC平分∠BOE,可求得∠COE=67°,∠EOF为直角,所以可得∠COF=∠EOF-∠EOC=23°;
(2)由(1)的方法即可得到∠COF=
;
(3)先设∠BOF为x°,再根据角的关系得出方程,解答后求出n的值即可.
(2)由(1)的方法即可得到∠COF=
| n° |
| 2 |
(3)先设∠BOF为x°,再根据角的关系得出方程,解答后求出n的值即可.
解答:解:(1)∵∠AOE=46°,
∴∠BOE=134°,
∵OC平分∠BOE,
∴∠COE=67°,
∵∠EOF为直角,
∴∠COF=∠EOF-∠EOC=23°,
故答案为:23;
(2))∵∠AOE=n°,
∴∠BOE=180°-n°,
∵OC平分∠BOE,
∴∠COE=
(180°-n°),
∵∠EOF为直角,
∴∠COF=∠EOF-∠EOC=90°-
(180°-n°)=
n°,
故答案为:
n°;
(3)设∠BOF为x°,∠AOD为(x+15)°,∠EOB为(90-x)°,OC平分∠BOE,
则可得:∠AOD+∠DOC+∠EOB=∠AOB+∠EOC.
x+15+x+15+90-x=180+
×(90-x)
解得:x=70,
所以可得:∠EOB=(90-x)°=20°,
∠AOE=180°-∠EOB=180°-20°=160°,
故n的值是160.
故答案为:160
∴∠BOE=134°,
∵OC平分∠BOE,
∴∠COE=67°,
∵∠EOF为直角,
∴∠COF=∠EOF-∠EOC=23°,
故答案为:23;
(2))∵∠AOE=n°,
∴∠BOE=180°-n°,
∵OC平分∠BOE,
∴∠COE=
| 1 |
| 2 |
∵∠EOF为直角,
∴∠COF=∠EOF-∠EOC=90°-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
(3)设∠BOF为x°,∠AOD为(x+15)°,∠EOB为(90-x)°,OC平分∠BOE,
则可得:∠AOD+∠DOC+∠EOB=∠AOB+∠EOC.
x+15+x+15+90-x=180+
| 1 |
| 2 |
解得:x=70,
所以可得:∠EOB=(90-x)°=20°,
∠AOE=180°-∠EOB=180°-20°=160°,
故n的值是160.
故答案为:160
点评:本题考查了角平分线定义,邻补角定义,角的和差,准确识图是解题的关键.

练习册系列答案
相关题目
 在一幅长为80cm、宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是5400cm2,设金色纸边的宽为x cm,那么x满足的方程是( )
在一幅长为80cm、宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是5400cm2,设金色纸边的宽为x cm,那么x满足的方程是( )| A、x2+65x-350=0 |
| B、x2+130x-1400=0 |
| C、x2-65x-350=0 |
| D、x2-130x-1400=0 |
将二次函数y=x2的图象向左平移1个单位,所得图象的函数关系式为( )
| A、y=x2+1 |
| B、y=x2-1 |
| C、y=(x+1)2 |
| D、y=(x-1)2 |
 已知△ABC的三个顶点的坐标分别为A(2,-1)、B(1,3)、C(-4,-2),求△ABC的面积.
已知△ABC的三个顶点的坐标分别为A(2,-1)、B(1,3)、C(-4,-2),求△ABC的面积.