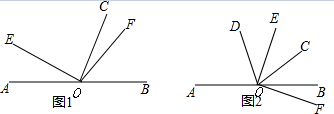题目内容
请你认真阅读下面的小探究系列,完成所提出的问题.
(1)探究1:如图1,点E、F分别在正方形ABCD边BC、CD上,AE⊥BF于点O,小芳看到该图后,发现AE=BF,这是因为∠EAB和∠FBC都是∠ABF的余角,就会由ASA判定得出△ABE≌△BCF.小芳马上联想到正方形的对角线也是互相垂直且相等的(如图2),是不是在一般情况下,正方形内部两条长度大于边长且互相垂直的线段,即使它们不经过正方形的顶点,也会相等呢?
很快她发现结果是成立的,除了通过构造法证明两条线段所在的三角形全等之外,还可以通过平移的方法把图3转化为图1,得到GH=EF,该方法更加简捷;
(2)探究2:小芳进一步思考,如果让两个全等正方形组成矩形ABCD,如图4所示,GH⊥EF于点O,她发现GH=2EF,请你替她完成证明;
(3)探究3:如图5所示,让8个全等正方形组成矩形ABCD,GH⊥EF于点O,请你猜想GH和EF有怎样的数量关系,写在下面: .
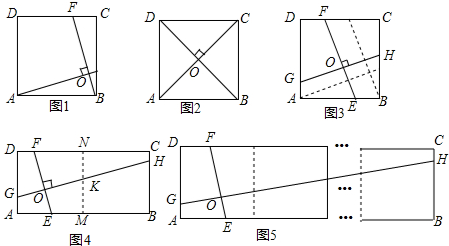
(1)探究1:如图1,点E、F分别在正方形ABCD边BC、CD上,AE⊥BF于点O,小芳看到该图后,发现AE=BF,这是因为∠EAB和∠FBC都是∠ABF的余角,就会由ASA判定得出△ABE≌△BCF.小芳马上联想到正方形的对角线也是互相垂直且相等的(如图2),是不是在一般情况下,正方形内部两条长度大于边长且互相垂直的线段,即使它们不经过正方形的顶点,也会相等呢?
很快她发现结果是成立的,除了通过构造法证明两条线段所在的三角形全等之外,还可以通过平移的方法把图3转化为图1,得到GH=EF,该方法更加简捷;
(2)探究2:小芳进一步思考,如果让两个全等正方形组成矩形ABCD,如图4所示,GH⊥EF于点O,她发现GH=2EF,请你替她完成证明;
(3)探究3:如图5所示,让8个全等正方形组成矩形ABCD,GH⊥EF于点O,请你猜想GH和EF有怎样的数量关系,写在下面:

考点:四边形综合题,相似三角形的判定与性质
专题:探究型
分析:(2)平移FE至DE′,平移GH至AH′,根据平移的性质可得:FE=DE′,GH=AH′,FE∥DE′,GH∥AH′,易证Rt△BAH′∽Rt△ADE′,然后运用相似三角形的性质就可解决问题.
(3)借鉴(2)中的解题经验可得
=
=
=8,则有GH=8EF.
(3)借鉴(2)中的解题经验可得
| GH |
| EF |
| AH′ |
| DE′ |
| AB |
| AD |
解答:(2)证明:平移FE至DE′,平移GH至AH′,如图4.
根据平移的性质可得:FE=DE′,GH=AH′,FE∥DE′,GH∥AH′,
∴四边形OPQR为平行四边形.
∵GH⊥EF,即∠POR=90°,
∴平行四边形OPQR为矩形,
∴∠AQE′=∠PQR=90°,
∴∠QAE′+∠QE′A=90°.
又∵∠ADE′+∠DE′A=90°,
∴∠ADE′=∠QAE′.
又∵∠DAE′=∠ABH′=90°,
∴Rt△BAH′∽Rt△ADE′,
∴
=
=2,
∴
=
=2,
∴GH=2EF.
(3)猜想:GH=8EF.
解:平移FE至DE′,平移GH至AH′,如图5.
根据平移的性质可得:FE=DE′,GH=AH′,FE∥DE′,GH∥AH′,
∴四边形OPQR为平行四边形.
∵GH⊥EF,即∠POR=90°,
∴平行四边形OPQR为矩形,
∴∠AQE′=∠PQR=90°,
∴∠QAE′+∠QE′A=90°.
又∵∠ADE′+∠DE′A=90°,
∴∠ADE′=∠QAE′.
又∵∠DAE′=∠ABH′=90°,
∴Rt△BAH′∽Rt△ADE′,
∴
=
=8,
∴
=
=8,
∴GH=8EF.
故答案为:GH=8EF.
根据平移的性质可得:FE=DE′,GH=AH′,FE∥DE′,GH∥AH′,
∴四边形OPQR为平行四边形.
∵GH⊥EF,即∠POR=90°,
∴平行四边形OPQR为矩形,

∴∠AQE′=∠PQR=90°,
∴∠QAE′+∠QE′A=90°.
又∵∠ADE′+∠DE′A=90°,
∴∠ADE′=∠QAE′.
又∵∠DAE′=∠ABH′=90°,
∴Rt△BAH′∽Rt△ADE′,
∴
| AH′ |
| DE′ |
| AB |
| AD |
∴
| GH |
| EF |
| AH′ |
| DE′ |
∴GH=2EF.
(3)猜想:GH=8EF.
解:平移FE至DE′,平移GH至AH′,如图5.
根据平移的性质可得:FE=DE′,GH=AH′,FE∥DE′,GH∥AH′,

∴四边形OPQR为平行四边形.
∵GH⊥EF,即∠POR=90°,
∴平行四边形OPQR为矩形,
∴∠AQE′=∠PQR=90°,
∴∠QAE′+∠QE′A=90°.
又∵∠ADE′+∠DE′A=90°,
∴∠ADE′=∠QAE′.
又∵∠DAE′=∠ABH′=90°,
∴Rt△BAH′∽Rt△ADE′,
∴
| AH′ |
| DE′ |
| AB |
| AD |
∴
| GH |
| EF |
| AH′ |
| DE′ |
∴GH=8EF.
故答案为:GH=8EF.
点评:本题考查了平移的性质、正方形的性质、矩形的性质、相似三角形的判定与性质等知识,突出了对基本活动经验的考查.

练习册系列答案
相关题目
下列说法错误的是( )
| A、任何有理数都有倒数 |
| B、互为倒数的两个数的积为1 |
| C、互为倒数的两个数同号 |
| D、-1的倒数是-1 |
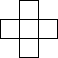 用8个相同的小正方形搭成一个几何体,其俯视图如图所示,那么这个几何体的左视图一定不是( )
用8个相同的小正方形搭成一个几何体,其俯视图如图所示,那么这个几何体的左视图一定不是( )