题目内容
若a、b、c是△ABC的三边,且关于x的方程x2-
x+1=0没有实数根,化简
+
+|2b+2c-8|= .
| b+c |
| (a+b+c)2 |
| (a-b-c)2 |
考点:二次根式的性质与化简,根的判别式,三角形三边关系
专题:
分析:首先利用根的判别式得出b+c<4,进而利用三角形三边关系以及二次根式的性质化简各式求出即可.
解答:解:∵关于x的方程x2-
x+1=0没有实数根,
∴b2-4ac=b+c-4<0,
即b+c<4,
∵a、b、c是△ABC的三边,
∴a+b+c>0,a-b-c<0,2b+2c-8<0,
∴
+
+|2b+2c-8|
=a+b+c-a+b+c-2b-2c+8
=8.
故答案为:8.
| b+c |
∴b2-4ac=b+c-4<0,
即b+c<4,
∵a、b、c是△ABC的三边,
∴a+b+c>0,a-b-c<0,2b+2c-8<0,
∴
| (a+b+c)2 |
| (a-b-c)2 |
=a+b+c-a+b+c-2b-2c+8
=8.
故答案为:8.
点评:此题主要考查了根的判别式和二次根式的性质等知识,正确化简各式是解题关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,已知∠1=∠2,若添一个条件就能使△ADE∽△ABC成立,则条件不能是( )
如图,已知∠1=∠2,若添一个条件就能使△ADE∽△ABC成立,则条件不能是( )| A、AD:AB=DE:BC |
| B、∠AED=∠C |
| C、∠D=∠B |
| D、AD:AB=AE:AC |
数-8不属于下列集合中的( )
| A、整数集合 | B、负数集合 |
| C、有理数集合 | D、非负数集合 |
 如图,经过△ABC两顶点B,C的⊙O与AB,AC分别交于点D,E,求证:AD•AB=AE•AC.
如图,经过△ABC两顶点B,C的⊙O与AB,AC分别交于点D,E,求证:AD•AB=AE•AC.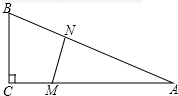 如图,在△ABC中,∠C=90°,BC=5米,AC=12米.点M在线段CA上,从C向A运动,速度为1米/秒;同时点N在线段AB上,从A向B运动,速度为2米/秒,运动时间为t秒.
如图,在△ABC中,∠C=90°,BC=5米,AC=12米.点M在线段CA上,从C向A运动,速度为1米/秒;同时点N在线段AB上,从A向B运动,速度为2米/秒,运动时间为t秒.