题目内容
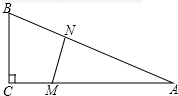 如图,在△ABC中,∠C=90°,BC=5米,AC=12米.点M在线段CA上,从C向A运动,速度为1米/秒;同时点N在线段AB上,从A向B运动,速度为2米/秒,运动时间为t秒.
如图,在△ABC中,∠C=90°,BC=5米,AC=12米.点M在线段CA上,从C向A运动,速度为1米/秒;同时点N在线段AB上,从A向B运动,速度为2米/秒,运动时间为t秒.(1)当t为何值时,∠AMN=∠ANM;
(2)当t为何值时,△ABC与△AMN相似?
考点:相似三角形的判定,等腰三角形的性质
专题:
分析:(1)由条件可知AM=12-t,AN=2t,利用条件可得到AM=AN,从而可得到关于t的方程,可求出t;
(2)当∠MNA=90°时,可得
=
,当∠NMA=90°时,有
=
,分别代入可得到关于t的方程,可求得t.
(2)当∠MNA=90°时,可得
| AN |
| AC |
| AM |
| AB |
| AN |
| AB |
| AM |
| AC |
解答:解:
(1)∵BC=5米,AC=12米,
∴AM=12-t,AN=2t,
若∠AMN=∠ANM,则AM=AN,
即12-t=2t,
解得t=4秒
即当t为4秒时,∠AMN=∠ANM;
(2)∵∠C=90°,
∴当△ABC和△AMN相似时,有∠MNA=90°和∠NMA=90°两种情况,且可求得AB=13,
当∠MNA=90°时,可得
=
,即
=
,解得t=
;
当∠NMA=90°时,可得
=
,即
=
,解得t=
;
即当t为
秒或
秒时,△ABC与△AMN相似.
(1)∵BC=5米,AC=12米,
∴AM=12-t,AN=2t,
若∠AMN=∠ANM,则AM=AN,
即12-t=2t,
解得t=4秒
即当t为4秒时,∠AMN=∠ANM;
(2)∵∠C=90°,
∴当△ABC和△AMN相似时,有∠MNA=90°和∠NMA=90°两种情况,且可求得AB=13,
当∠MNA=90°时,可得
| AN |
| AC |
| AM |
| AB |
| 2t |
| 12 |
| 12-t |
| 13 |
| 72 |
| 19 |
当∠NMA=90°时,可得
| AN |
| AB |
| AM |
| AC |
| 2t |
| 13 |
| 12-t |
| 12 |
| 156 |
| 37 |
即当t为
| 72 |
| 19 |
| 156 |
| 37 |
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,注意利用时间t表示出线段的长,化动为静是这类问题的一般思路.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
下列算式中错误的是( )
A、-
| |||||||
B、
| |||||||
C、±
| |||||||
D、
|
下列各式中,计算结果为正的是( )
| A、(-7)+(+4) | ||||
| B、2.7+(-3.5) | ||||
C、(-
| ||||
D、0+(-
|

 用火柴棒摆正方形,如图,则摆n个正方形要
用火柴棒摆正方形,如图,则摆n个正方形要