题目内容
16.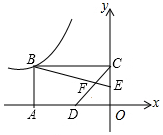 如图,双曲线y=-$\frac{42}{x}$的图象经过矩形OABC的顶点B,两边OA,OC在坐标轴上,且OD=$\frac{1}{3}$OA,E为OC的中点,BE与CD交于点F,则四边形EFDO的面积为$\frac{11}{2}$.
如图,双曲线y=-$\frac{42}{x}$的图象经过矩形OABC的顶点B,两边OA,OC在坐标轴上,且OD=$\frac{1}{3}$OA,E为OC的中点,BE与CD交于点F,则四边形EFDO的面积为$\frac{11}{2}$.
分析 先过E作EG∥OD,交CD于G,根据OD=$\frac{1}{3}$OA,E为OC的中点,求得S△CEF=$\frac{1}{7}$S△BCE,再根据矩形OABC的面积为42,即可得到△CEF和△COD的面积,进而得到四边形EFDO的面积.
解答  解:如图,过E作EG∥OD,交CD于G,
解:如图,过E作EG∥OD,交CD于G,
∵E为OC的中点,
∴EG=$\frac{1}{2}$OD,
∵OD=$\frac{1}{3}$OA,
∴EF=$\frac{1}{6}$OA=$\frac{1}{6}$BC,
即$\frac{EG}{BC}$=$\frac{1}{6}$,
∵EF∥AO∥BC,
∴$\frac{EF}{BF}$=$\frac{EG}{BC}$=$\frac{1}{6}$,
即EF=$\frac{1}{7}$BE,
∴S△CEF=$\frac{1}{7}$S△BCE,
∵双曲线y=-$\frac{42}{x}$的图象经过矩形OABC的顶点B,
∴矩形OABC的面积为42,
∴△BCE的面积为42×$\frac{1}{4}$=$\frac{21}{2}$,
∴S△CEF=$\frac{1}{7}$S△BCE=$\frac{1}{7}$×$\frac{21}{2}$=$\frac{3}{2}$,
∵OD=$\frac{1}{3}$OA,
∴S△COD=$\frac{1}{6}$S矩形AOCB=7,
∴四边形EFDO的面积=7-$\frac{3}{2}$=$\frac{11}{2}$,
故答案为:$\frac{11}{2}$.
点评 本题考查了反比例函数系数k的几何意义以及平行线分线段成比例定理的运用,关键是根据反比例函数系数k求出矩形的面积.在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

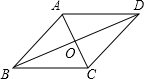 如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )
如图,四边形ABCD的对角线互相平分,若添加下列条件之一,不能使它变为菱形的条件是( )| A. | AB=AD | B. | AC=BD | C. | BD平分∠ABC | D. | AC⊥BD |
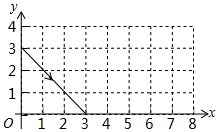 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P第17次碰到矩形的边时,点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角.当点P第17次碰到矩形的边时,点P的坐标为( )| A. | (3,0) | B. | (0,3) | C. | (1,4) | D. | (8,3) |
| A. | $\frac{1}{28}$ | B. | $\frac{1}{29}$ | C. | $\frac{1}{30}$ | D. | $\frac{1}{31}$ |
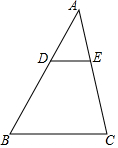 如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
如图,D、E分别是△ABC的边AB、AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )| A. | 4 | B. | 8 | C. | $\frac{21}{2}$ | D. | $\frac{25}{2}$ |