题目内容
 如图,将含有30°的Rt△AMF水平放置,将△AMF绕点A逆时针旋转得△AM1F1,AF1交FM于点K,设旋转角为β(0°<β<90°).
如图,将含有30°的Rt△AMF水平放置,将△AMF绕点A逆时针旋转得△AM1F1,AF1交FM于点K,设旋转角为β(0°<β<90°).(1)当△AFK为等腰三角形时,旋转角的度数为
(2)连接FF1,当△FKF1为等腰三角形时,你能求出△FKF1各内角的度数吗?
考点:旋转的性质,等腰三角形的判定
专题:计算题
分析:(1)由于△AFK为等腰三角形,根据等腰三角形的性质得∠FAK=∠AFM=30°,再根据旋转的性质得∠F1AF等于旋转角,于是得到旋转角为30°;
(2)根据旋转的性质得AF1=AF,再根据等腰三角形的性质得∠AFF1=∠AF1F,然后分类讨论:当FF1=FK时,则∠FKF1=∠FF1K,根据三角形外角性质得∠FKF1=β+30°,则∠FF1K=β+30°,所以∠AFF1=β+30°,则∠KFF1=β,在△KFF1中,根据三角形内角和定理可计算出β=40°,于是得到∠KFF1=40°,∠FKF1=70°,∠FF1K=70°;当F1F=F1K时,则∠FKF1=∠F1FK=30°+β,则∠AFF1=∠AF1F=30°+30°+β=60°+β,在△KFF1中,根据三角形内角和定理可计算出β=20°,易得∠KFF1=50°,∠FKF1=50°,∠FF1K=80°.
(2)根据旋转的性质得AF1=AF,再根据等腰三角形的性质得∠AFF1=∠AF1F,然后分类讨论:当FF1=FK时,则∠FKF1=∠FF1K,根据三角形外角性质得∠FKF1=β+30°,则∠FF1K=β+30°,所以∠AFF1=β+30°,则∠KFF1=β,在△KFF1中,根据三角形内角和定理可计算出β=40°,于是得到∠KFF1=40°,∠FKF1=70°,∠FF1K=70°;当F1F=F1K时,则∠FKF1=∠F1FK=30°+β,则∠AFF1=∠AF1F=30°+30°+β=60°+β,在△KFF1中,根据三角形内角和定理可计算出β=20°,易得∠KFF1=50°,∠FKF1=50°,∠FF1K=80°.
解答:解:(1)∵∠AFM=30°,
而△AFK为等腰三角形,
∴∠FAK=∠AFM=30°,
∵△AMF绕点A逆时针旋转得△AM1F1,
∴∠F1AF等于旋转角,即旋转角为30°;
故答案为30°;
(2)∵△AMF绕点A逆时针旋转得△AM1F1,
∴AF1=AF,
∴∠AFF1=∠AF1F,
当FF1=FK时,则∠FKF1=∠FF1K,
∵∠FKF1=β+30°,
∴∠FF1K=β+30°,
∴∠AFF1=β+30°,
∴∠KFF1=β,
在△KFF1中,30°+β+30°+β+β=180°,解得β=40°,
∴∠KFF1=40°,∠FKF1=70°,∠FF1K=70°;
当F1F=F1K时,则∠FKF1=∠F1FK=30°+β,
∴∠AFF1=∠AF1F=30°+30°+β=60°+β,
在△KFF1中,60°+β+30°+β+30°+β=180°,解得β=20°,
∴∠KFF1=50°,∠FKF1=50°,∠FF1K=80°,
综上所述,△FKF1各内角的度数分别为40°、70°、70°或50°、50°、80°.
而△AFK为等腰三角形,
∴∠FAK=∠AFM=30°,
∵△AMF绕点A逆时针旋转得△AM1F1,
∴∠F1AF等于旋转角,即旋转角为30°;
故答案为30°;
(2)∵△AMF绕点A逆时针旋转得△AM1F1,
∴AF1=AF,
∴∠AFF1=∠AF1F,
当FF1=FK时,则∠FKF1=∠FF1K,
∵∠FKF1=β+30°,
∴∠FF1K=β+30°,
∴∠AFF1=β+30°,
∴∠KFF1=β,
在△KFF1中,30°+β+30°+β+β=180°,解得β=40°,
∴∠KFF1=40°,∠FKF1=70°,∠FF1K=70°;
当F1F=F1K时,则∠FKF1=∠F1FK=30°+β,
∴∠AFF1=∠AF1F=30°+30°+β=60°+β,
在△KFF1中,60°+β+30°+β+30°+β=180°,解得β=20°,
∴∠KFF1=50°,∠FKF1=50°,∠FF1K=80°,
综上所述,△FKF1各内角的度数分别为40°、70°、70°或50°、50°、80°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
下列各组数中互为相反数的是( )
A、-2与
| |||
B、-2与
| |||
C、-2与-
| |||
| D、2与|-2| |
 四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,求证:∠BEC=30°.
四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,求证:∠BEC=30°.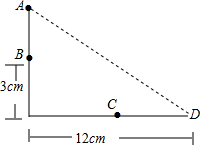 如图,在一颗树的B处有两只猴子,其中一只爬下来走向离树12m处的池塘,而另一个到树顶后直扑池塘(假设沿直线直扑).如果两只猴子的距离相等,那么这棵树有多高?
如图,在一颗树的B处有两只猴子,其中一只爬下来走向离树12m处的池塘,而另一个到树顶后直扑池塘(假设沿直线直扑).如果两只猴子的距离相等,那么这棵树有多高?