题目内容
20．
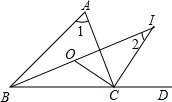△ABC中，∠ABC=40°，∠ACB=80°，BO、CO分别平分∠ABC，∠ACB，交于O，CI为外角∠ACD的平分线，BO的延长线交CI于I点，记∠BAC=∠1，∠BIC=∠2，则∠1：∠2=2：1（求比值）．
分析 根据三角形的一个外角等于与它不相邻的两个内角的和列式表示出∠ACD和∠ICD，再根据角平分线的定义表示出∠IBC和∠ICD，然后整理即可得解．
解答 解：根据三角形的外角性质，∠ACD=∠A+∠ABC，∠ICD=∠I+∠IBC，
∵BI、CI分别平分∠ABC和∠ACD，
∴∠IBC=$\frac{1}{2}$∠ABC，∠ICD=$\frac{1}{2}$∠ACD，
∴∠I+$\frac{1}{2}$∠ABC=$\frac{1}{2}$（∠A+∠ABC），
∴∠I=$\frac{1}{2}$∠A，
∴∠1：∠2=2：1；
故答案为：2：1．
点评 本题考查了三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，以及角平分线的定义．
练习册系列答案
相关题目
10．下列根式中，最简二次根式是（ ）
| A． | $\sqrt{9a}$ | B． | $\sqrt{{a^2}+{b^2}}$ | C． | $\sqrt{\frac{a}{3}}$ | D． | $\sqrt{0.5}$ |
11．下列是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}x-y=1\\ \frac{1}{x}+y=4\end{array}$ | B． | $\left\{\begin{array}{l}{x+y=4}\\{{x}^{2}+{y}^{2}=9}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}x+y=4\\ xy=4\end{array}$ | D． | $\left\{\begin{array}{l}3x+5y=25\\ x+10y=25\end{array}$ |
