题目内容
12. 在纸上剪下一个圆和一个扇形纸片,使它们恰好围成一个圆锥(如图所示),如果扇形的圆心角为90°,扇形的半径为16,那么所围成的圆锥的高为4$\sqrt{15}$.
在纸上剪下一个圆和一个扇形纸片,使它们恰好围成一个圆锥(如图所示),如果扇形的圆心角为90°,扇形的半径为16,那么所围成的圆锥的高为4$\sqrt{15}$.
分析 设圆锥的底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=$\frac{90•π•16}{180}$,解得r=4,然后利用扇形的半径等于圆锥的母线长和勾股定理计算圆锥的高.
解答 解:设圆锥的底面圆的半径为r,
根据题意得2πr=$\frac{90•π•16}{180}$,解得r=4,
所以所围成的圆锥的高=$\sqrt{1{6}^{2}-{4}^{2}}$=4$\sqrt{15}$.
故答案为4$\sqrt{15}$.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了弧长公式和勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.关于x的一元二次方程$\sqrt{2}{x^2}+\sqrt{2}{a^2}=3ax$的两根应为( )
| A. | $\frac{{-\sqrt{2}±a}}{{\sqrt{2}}}$ | B. | $\sqrt{2}a$,$\frac{{\sqrt{2}}}{2}a$ | C. | $\frac{{2±\sqrt{2}a}}{4}$ | D. | $±\sqrt{2}a$ |
7.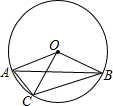 如图,OA,OB,OC都是⊙O的半径,如果∠CAB=2∠CBA,那么下列结论正确的是( )
如图,OA,OB,OC都是⊙O的半径,如果∠CAB=2∠CBA,那么下列结论正确的是( )
 如图,OA,OB,OC都是⊙O的半径,如果∠CAB=2∠CBA,那么下列结论正确的是( )
如图,OA,OB,OC都是⊙O的半径,如果∠CAB=2∠CBA,那么下列结论正确的是( )| A. | ∠OCB=2∠OAB | B. | ∠BOC=2∠AOC | C. | BC=2AC | D. | AB=2AC |
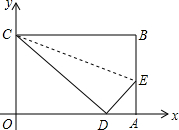 如图,矩形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,OA=10、OC=8,
如图,矩形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,OA=10、OC=8, 如图,△ABC∽△DEF,若∠B=50°,则∠E的度数是50度.
如图,△ABC∽△DEF,若∠B=50°,则∠E的度数是50度.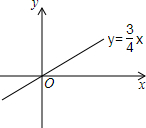 如图,直线y=$\frac{3}{4}$x的图象与抛物线y=ax2-4ax+c交于A、B两点(其中点A在点B的左侧),且与此抛物线的对称轴交于点C.
如图,直线y=$\frac{3}{4}$x的图象与抛物线y=ax2-4ax+c交于A、B两点(其中点A在点B的左侧),且与此抛物线的对称轴交于点C.