题目内容
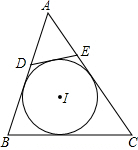 如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为( )
如图,⊙I为△ABC的内切圆,点D,E分别为边AB,AC上的点,且DE为⊙I的切线,若△ABC的周长为20,BC边的长为6,则△ADE的周长为( )| A、15 | B、9 | C、8 | D、7.5 |
考点:三角形的内切圆与内心
专题:计算题
分析:如图,⊙I与△ABC和DE相切的切点分别为G、K、H、F,根据切线长定理得到DG=DF,EF=EH,BG=BK,CK=CH,则△ADE的周长=AD+AE+DE=AD+AE+DG+EH=AG+AH,再利用△ABC的周长为20得到AG+AH+BG+BK+CK+CH=20,利用等线段代换可得AG+AH+BK+BK+CK+CK=20,则有AG+AH+2BC=20,所以AG+AH=8,即△ADE的周长为8.
解答:解:如图, ⊙I与△ABC和DE相切的切点分别为G、K、H、F,
⊙I与△ABC和DE相切的切点分别为G、K、H、F,
则DG=DF,EF=EH,BG=BK,CK=CH,
△ADE的周长=AD+AE+DE=AD+AE+DF+EF=AD+AE+DG+EH=AG+AH,
∵△ABC的周长为20,
∴AG+AH+BG+BK+CK+CH=20,
∴AG+AH+BK+BK+CK+CK=20,
即AG+AH+2(BK+CK)=20,
∴AG+AH+2BC=20,
而BC=6,
∴AG+AH=60-2×6=8,
∴△ADE的周长为8.
故选C.
 ⊙I与△ABC和DE相切的切点分别为G、K、H、F,
⊙I与△ABC和DE相切的切点分别为G、K、H、F,则DG=DF,EF=EH,BG=BK,CK=CH,
△ADE的周长=AD+AE+DE=AD+AE+DF+EF=AD+AE+DG+EH=AG+AH,
∵△ABC的周长为20,
∴AG+AH+BG+BK+CK+CH=20,
∴AG+AH+BK+BK+CK+CK=20,
即AG+AH+2(BK+CK)=20,
∴AG+AH+2BC=20,
而BC=6,
∴AG+AH=60-2×6=8,
∴△ADE的周长为8.
故选C.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了切线长定理.

练习册系列答案
相关题目
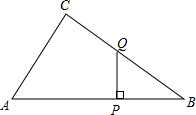 如图所示,在Rt△ABC中,∠ACB=90°,P为AB边上一点,Q为BC边上一点.PQ⊥AB,垂足为P,且△BPQ的面积等于四边形APQC面积的
如图所示,在Rt△ABC中,∠ACB=90°,P为AB边上一点,Q为BC边上一点.PQ⊥AB,垂足为P,且△BPQ的面积等于四边形APQC面积的 如图,AD∥EF∥BC,EF分别与AB,DC,AC,BD相交于点E、F、G、H,EH与FG相等吗?为什么?
如图,AD∥EF∥BC,EF分别与AB,DC,AC,BD相交于点E、F、G、H,EH与FG相等吗?为什么? 如图,已知∠B=45°,∠A=30°,∠C=25°,求∠ADC的大小.
如图,已知∠B=45°,∠A=30°,∠C=25°,求∠ADC的大小. 尺规画图 (不用写作法,要保留作图痕迹)
尺规画图 (不用写作法,要保留作图痕迹)