题目内容
 (1)如图1,已知:∠2=∠3,∠1+∠3=180°,
(1)如图1,已知:∠2=∠3,∠1+∠3=180°,求证:EF∥GH,AB∥CD.
证明:∵∠2=∠3,∠1+∠3=180°(已知)
∴∠1+∠2=180°(理由:
所以EF∥GH.(理由:
∵∠2=∠3(已知)
∴AB∥CD(理由:
(2)如图2,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E.
证明:∵
∴∠ABD=∠BDC ( 根据:
由AE∥BD.
得∠BDC=∠E.(根据:
再根据:等量代换得:∠ABD=∠E.
考点:平行线的判定与性质
专题:推理填空题
分析:(1)根据过程分别写出每一步的理由即可;
(2)根据平行线的性质和判定写出理由即可.
(2)根据平行线的性质和判定写出理由即可.
解答:(1)证明:∵∠2=∠3,∠1+∠3=180°(已知),
∴∠1+∠2=180°(理由:等量代换),
所以EF∥GH.(理由:同旁内角互补,两直线平行),
∵∠2=∠3(已知),
∴AB∥CD(理由:同位角相等,两直线平行);
故答案为:等量代换,同旁内角互补,两直线平行,同位角相等,两直线平行;
(2)证明:∵AB∥CD(已知),
∴∠ABD=∠BDC ( 根据:两直线平行,内错角相等),
由AE∥BD.
得∠BDC=∠E.(根据:两直线平行,同位角相等).
再根据:等量代换得:∠ABD=∠E.
故答案为:AB∥CD,两直线平行,内错角相等,两直线平行,同位角相等.
∴∠1+∠2=180°(理由:等量代换),
所以EF∥GH.(理由:同旁内角互补,两直线平行),
∵∠2=∠3(已知),
∴AB∥CD(理由:同位角相等,两直线平行);
故答案为:等量代换,同旁内角互补,两直线平行,同位角相等,两直线平行;
(2)证明:∵AB∥CD(已知),
∴∠ABD=∠BDC ( 根据:两直线平行,内错角相等),
由AE∥BD.
得∠BDC=∠E.(根据:两直线平行,同位角相等).
再根据:等量代换得:∠ABD=∠E.
故答案为:AB∥CD,两直线平行,内错角相等,两直线平行,同位角相等.
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是本题的关键,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个数的相反数是它本身,则这个数是( )
| A、正数 | B、负数 | C、0 | D、负数和0 |
把π≈3.1415926…按四舍五入法精确到0.0001的近似值为( )
| A、3.1415 |
| B、3.1416 |
| C、3.142 |
| D、3.1417 |
 李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图,那么到达乙地时油箱剩余油量是( )升.
李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图,那么到达乙地时油箱剩余油量是( )升. 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连结CD、OD,给出以下四个结论:
如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连结CD、OD,给出以下四个结论: 如图,在?ABCD中,E、F分别是AB、CD上的点,且AE=CF,求证:四边形EBFD为平行四边形.
如图,在?ABCD中,E、F分别是AB、CD上的点,且AE=CF,求证:四边形EBFD为平行四边形.
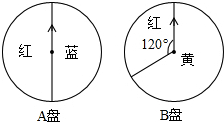 小颖和小明用如图所示的两个转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可配成紫色,此时小颖得2分,否则小明得1分.
小颖和小明用如图所示的两个转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可配成紫色,此时小颖得2分,否则小明得1分.