题目内容

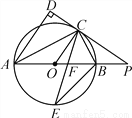
如图，AB 是⊙O 的直径，点C 是⊙O 上一点，AD 与过点C的切线垂直,垂足为 D，直线 DC 与AB 的延长线相交于点P，弦CE平分∠ACB，交AB 于点F，连接BE．

求证：(1)AC 平分∠DAB；

(2)△PCF 是等腰三角形．

详见解析. 【解析】试题分析：(1) AB 是⊙O 的直径，可得OC⊥PD，又AD⊥PD，得出OC∥AD，根据平行线的性质得到∠ACO＝∠DAC，又因AO=OC,得∠ACO＝∠CAO，所以AC 平分∠DAB；（2）根据弦切角定理得∠CAO＝∠PCB，又因弦CE 平分∠ACB，所以∠ACF＝∠BCF，所以根据外角的性质得∠PFC＝∠CAO+∠ACF，∠PCF=∠PCB+∠BCF，所以∠PFC＝...
练习册系列答案
相关题目

如图，抛物线的对称轴为直线x=－1，与y相交于（0，－6），则关于x的方程的解为（　　）

A. B. ，

C. ， D. ，

B 【解析】由于抛物线的对称轴为直线x=－1，与y相交于（0，－6），则其关于直线x=－1的对称点是（-2，-6）. 即的解 为， ，故选B.

如图，△ABC中，AB=AC=18，BC=12，正方形DEFG的顶点E，F在△ABC内，顶点D，G分别在AB，AC上，AD=AG，DG=6，则点F到BC的距离为．

A. 1 B. 2 C. D.

D 【解析】试题分析：过点A作BC的垂线得出高线为12，根据相似三角形的性质可得点A到DG的距离为6，则点F到BC的距离为：6－6.

“激情盛会，和谐亚洲”第16届亚运会将于2010年11月在广州举行，广州亚运城的建筑面积约是358 000平方米，将358 000用科学记数法表示为______．

3.58×105 【解析】科学记数法的一般形式为：a×10n，在本题中a应为3.58，10的指数为7-1=6． 【解析】 3580000=3.58×106． 科学记数法是每年中考试卷中的必考问题，把一个数写成a×106的形式（其中1≤|a|＜10，n为整数），这种计数法称为科学记数法．其方法是（1）确定a：a是只有一位整数的数；（2）确定n：当原数的绝对值≥10时，n为正整数，...

抛物线y=﹣x2+bx+c的部分图象如图所示，要使y＞0，则x的取值范围是（　　）

A. ﹣4＜x＜1 B. ﹣3＜x＜1 C. x＜﹣4或x＞1 D. x＜﹣3或x＞1

B 【解析】由抛物线的对称性可知抛物线与x轴另一个交点的坐标为（-3，0），从图象可知当-30；故选B.

“五段彩虹展翅飞”,横跨南渡江的琼州大桥如图,该桥的两边均有五个红色的圆拱,如图(1)．最高的圆拱的跨度为110m,拱高为22m,如图(2),那么这个圆拱所在圆的直径为多少米?

159.5m． 【解析】试题分析：在三角形OCF中可求得OF=OE-EF,OE=OC，所以根据勾股定理可得OC2=OF2+CF2，CF=CD,求出半径OC的长，进而求出直径. 设所在圆的圆心为O,作OE⊥CD 于点F,交圆拱于点E, 连接OC．设圆拱的半径为rm,则OF＝(r－22)m． ∵OE⊥CD,∴CF＝CD＝×110＝55(m)． 根据勾股定理,得OC2＝CF...

如图，AB是⊙O的直径，点C是⊙O上的一点，若BC=6，AB=10，OD⊥BC于点D，则OD的长为______．

4 【解析】试题分析：根据垂径定理求得BD，然后根据勾股定理求得即可． 【解析】 ∵OD⊥BC， ∴BD=CD=BC=3， ∵OB=AB=5， ∴OD==4． 故答案为4．

四张大小、质地均相同的卡片上分别标有数字1，2，3，4，现将标有数字的一面朝下扣在桌子上，从中随机抽取一张（不放回），再从桌子上剩下的3张中随机抽取第二张.

（1）用画树状图的方法，列出前后两次抽得的卡片上所标数字的所有可能情况；

（2）计算抽得的两张卡片上的数字之积为奇数的概率是多少？

（1） （2）P（积为奇数）= 【解析】（1）用树状图列举出2次不放回实验的所有可能情况即可； （2）看是奇数的情况占所有情况的多少即可．

用直接开平方法解方程：

(1) 4(x－2)2－36＝0；

(2) x2＋6x＋9＝25；

(3) 4(3x－1)2－9(3x＋1)2＝0.

(1) x1＝5，x2＝－1；（2）x1＝－8，x2＝2；（3）x1＝－，x2＝－ 【解析】试题分析： （1）先移项，系数化为1后，再用直接开平方求解； （2）左边因式分解为一个完全平方式后，再用直接开平方法求解； （3）先移项，再用直接开平方法求解. 试题解析： (1) 4(x－2)2－36＝0，(x－2)2=9，x-2=±3，所以x1＝5，x2＝－1； ...

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网