题目内容
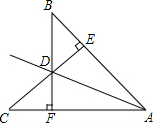 如图,BF⊥AC于F,CE⊥AB于E,BF和CE交于D,且BE=CF,求证:AD平分∠BAC.
如图,BF⊥AC于F,CE⊥AB于E,BF和CE交于D,且BE=CF,求证:AD平分∠BAC.考点:角平分线的性质,全等三角形的判定与性质
专题:证明题
分析:先根据AAS定理得出△BDE≌△CDF,故可得出DF=DE,由此可得出结论.
解答:证明:∵BF⊥AC于F,CE⊥AB于E,
∴∠BED=∠CFD=90°.
在Rt△BDE与Rt△CDF中,
,
∴△BDE≌△CDF(AAS),
∴BE=CF,
∴AD平分∠BAC.
∴∠BED=∠CFD=90°.
在Rt△BDE与Rt△CDF中,
|
∴△BDE≌△CDF(AAS),
∴BE=CF,
∴AD平分∠BAC.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知∠A与∠B互余,若∠A=50°,则∠B的度数是( )
| A、40° | B、50° |
| C、130° | D、140° |
以下列各组线段为边,能组成三角形的是( )
| A、3cm,5cm,8cm |
| B、4cm,7cm,9cm |
| C、2cm,3cm,6cm |
| D、4cm,4cm,9cm |
若点P(a,b)在第四象限内,则a,b的取值范围是( )
| A、a>0,b<0 |
| B、a>0,b>0 |
| C、a<0,b>0 |
| D、a<0,b<0 |
若|x+2|+(y-3)2=0,则xy=( )
| A、-8 | B、-6 | C、6 | D、8 |
已知a、b、c是满足a2+2b=7,b2-2c=-1,c2-6a=-17,则a-b+c的值等于( )
| A、5 | B、4 | C、3 | D、2 |
 如图,若∠1=∠D,BD平分∠ABC,且∠ABC=55°,试求∠BCD的度数.
如图,若∠1=∠D,BD平分∠ABC,且∠ABC=55°,试求∠BCD的度数.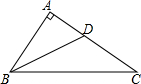 如图,在△ABC中,∠A=90°,BD是角平分线,若AD=m,BC=n,求△BCD的面积.
如图,在△ABC中,∠A=90°,BD是角平分线,若AD=m,BC=n,求△BCD的面积.