题目内容
已知a、b、c是满足a2+2b=7,b2-2c=-1,c2-6a=-17,则a-b+c的值等于( )
| A、5 | B、4 | C、3 | D、2 |
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:首先把a2+2b=7,b2-2c=-1,c2-6a=-17,两边相加整理成a2+2b+b2-2c+c2-6a+11=0,分解因式,利用非负数的性质得出a、b、c的数值,代入求得答案即可.
解答:解:∵a2+2b=7,b2-2c=-1,c2-6a=-17,
∴a2+2b+b2-2c+c2-6a+11=0,
∴(a-3)2+(b+1)2+(c-1)2=0,
∴a=3,b=-1,c=1,
∴a-b+c=5.
故选:A.
∴a2+2b+b2-2c+c2-6a+11=0,
∴(a-3)2+(b+1)2+(c-1)2=0,
∴a=3,b=-1,c=1,
∴a-b+c=5.
故选:A.
点评:此题考查了配方法,掌握完全平方公式是解决问题的关键..

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
以下各组数不能作为直角三角形的边长的是( )
| A、5,12,13 | ||||||
B、
| ||||||
| C、7,24,25 | ||||||
| D、8,15,17 |
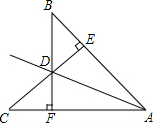 如图,BF⊥AC于F,CE⊥AB于E,BF和CE交于D,且BE=CF,求证:AD平分∠BAC.
如图,BF⊥AC于F,CE⊥AB于E,BF和CE交于D,且BE=CF,求证:AD平分∠BAC. 画出反比例函数y=-
画出反比例函数y=- 如图,∠ABC=∠ADC,DE分别是∠ABC,∠ADC的角平分线,∠1=∠2,求证:DC∥AB.
如图,∠ABC=∠ADC,DE分别是∠ABC,∠ADC的角平分线,∠1=∠2,求证:DC∥AB. 如图,平行四边形ABCD和平行四边形EAFC的顶点D,B,E,F在同一条直线上,求证:△ABF≌△CDE.
如图,平行四边形ABCD和平行四边形EAFC的顶点D,B,E,F在同一条直线上,求证:△ABF≌△CDE.