题目内容
若|x+2|+（y-3）2=0，则xy=（ ）
| A、-8 | B、-6 | C、6 | D、8 |
考点：代数式求值,非负数的性质：绝对值,非负数的性质：偶次方
专题：
分析：直接利用偶次方以及绝对值的性质得出x，y的值，进而求出答案．
解答：解：∵|x+2|+（y-3）2=0，
∴x+2=0，y-3=0，
解得：x=-2，y=3，
故xy=（-2）3=-8．
故选：A．
∴x+2=0，y-3=0，
解得：x=-2，y=3，
故xy=（-2）3=-8．
故选：A．
点评：此题主要考查了代数式求值，得出x，y的值是解题关键．
练习册系列答案
相关题目
墨墨发现从某多边形的一个顶点出发，可以作4条对角线，则这个多边形的内角和是（ ）
| A、1260° | B、1080° |
| C、900° | D、720° |
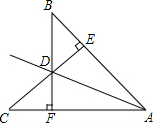如图，BF⊥AC于F，CE⊥AB于E，BF和CE交于D，且BE=CF，求证：AD平分∠BAC．
如图，一次函数y=-x+6的图象经过点P（a，b）和Q（c，d），则a（c+d）+b（c+d）的值为以下各组数不能作为直角三角形的边长的是（ ）
| A、5，12，13 | ||||||
B、
| ||||||
| C、7，24，25 | ||||||
| D、8，15，17 |
画出反比例函数y=-
如图，∠ABC=∠ADC，DE分别是∠ABC，∠ADC的角平分线，∠1=∠2，求证：DC∥AB．（-2）0的结果是（ ）
| A、-2 | B、-1 | C、0 | D、1 |