题目内容
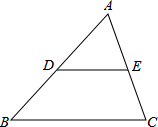 如图,在△ABC中,D、E分别为边AB、AC的中点.
如图,在△ABC中,D、E分别为边AB、AC的中点.(1)证明:△ADE∽△ABC;
(2)求△ADE与△ABC的相似的相似比.
考点:相似三角形的判定与性质
专题:
分析:(1)首先证明DE为△ABC的中位线,进而证明DE∥BC,问题即可解决.
(2)通过△ADE∽△ABC,列出比例式求解即可解决问题.
(2)通过△ADE∽△ABC,列出比例式求解即可解决问题.
解答: (1)证明:
(1)证明:
∵D、E分别为边AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,且DE=
BC,
∴△ADE∽△ABC.
(2)解:
∵△ADE∽△ABC,
∴
=
=
,
即△ADE与△ABC的相似的相似比为
.
 (1)证明:
(1)证明:∵D、E分别为边AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,且DE=
| 1 |
| 2 |
∴△ADE∽△ABC.
(2)解:
∵△ADE∽△ABC,
∴
| AD |
| AB |
| DE |
| BC |
| 1 |
| 2 |
即△ADE与△ABC的相似的相似比为
| 1 |
| 2 |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入观察、合情猜测、科学论证.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
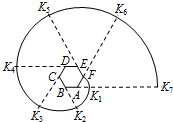 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中FK1,K1K2,K2K3,K3K4,K5K6…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2014等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
下列六种说法正确的个数是( )
①无限小数都是无理数; ②正数、负数统称有理数; ③无理数的相反数还是无理数;
④无理数与无理数的和一定还是无理数; ⑤无理数与有理数的和一定是无理数;
⑥有理数和无理数统称实数.
①无限小数都是无理数; ②正数、负数统称有理数; ③无理数的相反数还是无理数;
④无理数与无理数的和一定还是无理数; ⑤无理数与有理数的和一定是无理数;
⑥有理数和无理数统称实数.
| A、2个 | B、3个 | C、4个 | D、5个 |
在平面直角坐标系xOy中,已知点P(-3,3),点Q在x轴上,△PQO是等腰三角形,则满足条件的点Q共有( )
| A、5个 | B、4个 | C、3个 | D、2个 |
已知反比例函数图象经过点(2,-2),(-1,n),则n等于( )
| A、3 | B、4 | C、-3 | D、-4 |
 如图,圆内有弦AB,点C在半径为5的圆上,∠ACB=30°,点E,F分别是AC,BC的中点,直线EF交圆于G,H两点.那么GE+FH的最大值是( )
如图,圆内有弦AB,点C在半径为5的圆上,∠ACB=30°,点E,F分别是AC,BC的中点,直线EF交圆于G,H两点.那么GE+FH的最大值是( )