题目内容
已知一系列有规律的数:-2,3,-5,9,-17,33,其中第10个数是 .
考点:规律型:数字的变化类
专题:
分析:数字是2n-1+1,奇数位置为负,偶数位置为正,由此规律得出答案即可.
解答:解:-2=-(21-1+1)
3=22-1+1
-5=-(23-1+1)
9=24-1+1
-17=-(25-1+1)
33=26-1+1
…
那么,第n个数可表示为:(-1)n(2n-1+1).
当n=10即第10个数是210-1+1=513.
故答案为:513.
3=22-1+1
-5=-(23-1+1)
9=24-1+1
-17=-(25-1+1)
33=26-1+1
…
那么,第n个数可表示为:(-1)n(2n-1+1).
当n=10即第10个数是210-1+1=513.
故答案为:513.
点评:此题考查数字的变化规律,考查观察探究归纳问题的能力.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
下列各式:
,
(a≥2),
,
,-
,其中二次根式有( )个.
| x2+1 |
| a-2 |
| (x-1)2 |
| -3 |
| x2+1 |
| A、3个 | B、4个 | C、5个 | D、6个 |
下列运算中,正确的是( )
| A、(-a-2b)(a+2b)=a2-4b2 |
| B、(-a+2b)(a-2b)=-a2-2b2 |
| C、(a+2b)(a-2b)=-a2-2b2 |
| D、(-a-2b)(-a+2b)=a2-4b2 |
如果三个有理数的积是负数,那么这三个有理数中( )
| A、只有一个负数 |
| B、有两个负数 |
| C、三个都是负数 |
| D、有一个或三个负数 |
计算(-2)×(-3)的值为( )
| A、5 | B、-5 | C、6 | D、-6 |
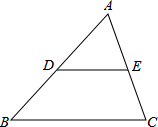 如图,在△ABC中,D、E分别为边AB、AC的中点.
如图,在△ABC中,D、E分别为边AB、AC的中点. 如图,在△ABC中,AB=4,点D在AB边上移动(不与A、B重合),DE∥BC,交AC于点E,设S△ABC=S,S△DEC=S1,若AD=x,
如图,在△ABC中,AB=4,点D在AB边上移动(不与A、B重合),DE∥BC,交AC于点E,设S△ABC=S,S△DEC=S1,若AD=x,